
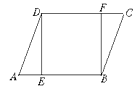
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y= ![]() x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.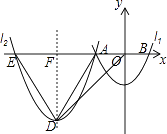
(1)求抛物线l2的解析式;
(2)求证:△ADE∽△DOE;
(3)半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
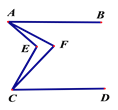
【题目】如图,已知AB‖CD,∠EAF =![]() ∠EAB,∠ECF=
∠EAB,∠ECF=![]() ∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
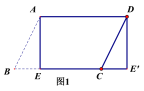
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
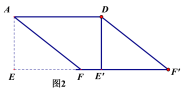
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两名运动员,选择一人参加市射击比赛,在选拔赛上,每人打10发,其中甲的射击成绩分别为10、8、7、9、8、10、10、9、10、9
①计算甲的射击成绩的方差;
②经过计算,乙射击的平均成绩是9,方差为1.4,你认为选谁去参加市射击比赛合适,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com