
【题目】如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y= ![]() x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.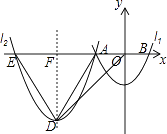
(1)求抛物线l2的解析式;
(2)求证:△ADE∽△DOE;
(3)半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.
【答案】
(1)
解:设抛物线l2的解析式为y= ![]() (x+a)2+c,
(x+a)2+c,
∵抛物线l2的对称轴为x=﹣6,
∴a=6.
令l1的解析式y= ![]() x2﹣2=0,
x2﹣2=0,
解得:x=±2.
∴A点的坐标为(﹣2,0),B点的坐标为(2,0).
将点A(﹣2,0)代入l2的解析式中,得 ![]() ×(﹣2+6)2+c=0,
×(﹣2+6)2+c=0,
解得:c=﹣8.
故抛物线l2的解析式为y= ![]() ﹣8
﹣8
(2)
证明:令l2的解析式y= ![]() ﹣8=0,
﹣8=0,
解得x=﹣10,或x=﹣2,
故点E的坐标为(﹣10,0).
由抛物线的对称性可知△ADE为等腰三角形.
∵点O(0,0),点E(﹣10,0),点D(﹣6,﹣8),
∴OE=0﹣(﹣10)=10,OD= ![]() =10,
=10,
∴OE=OD,
即△OED为等腰三角形,
又∵∠DEA=∠OED,且两者均为底角,
∴△ADE∽△DOE
(3)
解:过点C作CN⊥DF于点N,根据题意画出图形如图所示.

点D旋转后到达D′处,点F旋转后到达F′处.
根据旋转的性质可知D′F′=DF,
∵点D(﹣6,﹣8),点F(﹣6,0),
∴P1的运动路径长为DF=8.
∵DF∥y轴,
∴D′F′∥x轴,
∴四边形NCMD′为平行四边,
∴D′M=NC.
∵l1的解析式为y= ![]() x2﹣2,
x2﹣2,
∴点C的坐标为(0,﹣2),
∴点N的坐标为(﹣6,﹣2),
∴NC=0﹣(﹣6)=6.
∵⊙P1的半径为1,
∴当D′P1=D′M±1时,⊙P1与y轴相切,
此时D′P1=5,或D′P1=7.
∵⊙P的运动速度为1单位/秒,
∴⊙P1的运动速度为1单位/秒,
∴运算时间为5秒或7秒
【解析】(1)设抛物线l2的解析式为y= ![]() (x+a)2+c,由抛物线l1的解析式,可求出点A的坐标,由抛物线l2的对称轴以及点A的坐标即可求出a、c的值,由此得出结论;(2)由抛物线的对称性可知△DAE为等腰三角形,由l2的解析式可得出D点、E点坐标,根据两点间的距离公式可求出OE=OD,由两等腰三角形一个底角相等即可得出△ADE∽△DOE;(3)由旋转的特性可知P1的运动路径长与P的运动路径长相等,由圆与直线相切可得出相切时D′P1的长度,由时间=路程÷速度即可得出结论.
(x+a)2+c,由抛物线l1的解析式,可求出点A的坐标,由抛物线l2的对称轴以及点A的坐标即可求出a、c的值,由此得出结论;(2)由抛物线的对称性可知△DAE为等腰三角形,由l2的解析式可得出D点、E点坐标,根据两点间的距离公式可求出OE=OD,由两等腰三角形一个底角相等即可得出△ADE∽△DOE;(3)由旋转的特性可知P1的运动路径长与P的运动路径长相等,由圆与直线相切可得出相切时D′P1的长度,由时间=路程÷速度即可得出结论.


科目:初中数学 来源: 题型:
【题目】某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
次数 | 70≤x<90 | 90≤x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息,回答下列问题:
(1)本次调查的样本容量是;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有人;
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.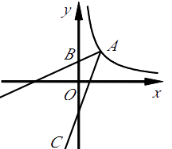
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③![]() ;④BD平分∠ADC;⑤∠BDC=
;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有_______个.
∠BAC.其中正确的结论有_______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架5米长的梯子AB斜靠在一面墙上,梯子底端B到墙底的垂直距离BC为3米.
(1)求这个梯子的顶端A到地面的距离AC的值;
(2)如果梯子的顶端A沿墙AC竖直下滑1米到点D处,求梯子的底端B在水平方向滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个只允许单向通过的窄道口,通常情况下,每分钟可以通过9人.一天王老师到达道口时,发现由于拥挤,每分钟只能有3人通过道口,此时,自己前面还有36人等待通过(假定先到达的先过,王老师过道口的时间忽略不计),通过道口后,还需7分钟到达学校.

(1)此时,若绕道而行,要15分钟才能到达学校,从节省时间考虑,王老师应选择绕道去学校,还是选择通过拥挤的道口去学校?
(2)若在王老师等人的维持下,几分钟后秩序恢复正常(维持秩序期间,每分钟仍有3人通过道口),结果王老师比在拥挤的情况下提前6分钟通过道口,问维持秩序的时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
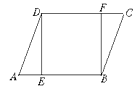
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com