
【题目】已知直线![]() 与x轴交于点A,与y轴交于点B,现将
与x轴交于点A,与y轴交于点B,现将![]() 沿直线AB翻折得到
沿直线AB翻折得到![]() ,以点A、B、C为顶点作平行四边形,第四个顶点D的坐标是______.
,以点A、B、C为顶点作平行四边形,第四个顶点D的坐标是______.
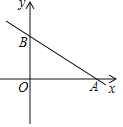
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】武警战士乘一冲锋舟从![]() 地逆流而上,前往
地逆流而上,前往![]() 地营救受困群众,途经
地营救受困群众,途经![]() 地时,由所携带的救生艇将
地时,由所携带的救生艇将![]() 地受困群众运回
地受困群众运回![]() 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到![]() 地接到群众后立刻返回
地接到群众后立刻返回![]() 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.

(1)请直接写出冲锋舟从![]() 地到
地到![]() 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将![]() 地群众安全送到
地群众安全送到![]() 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数关系式为
(分)之间的函数关系式为![]() ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离![]() 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,电力公司规定如下电费计算方法:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)若某用户某年1月交电费88元,那么该用户1月份用电多少度?
(2)若某用户某年2月份平均每度电费0.75元,那么该用户2月份用电多少度?应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y= ![]() x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.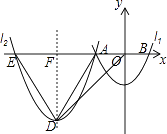
(1)求抛物线l2的解析式;
(2)求证:△ADE∽△DOE;
(3)半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 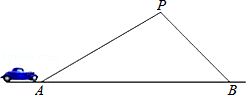
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
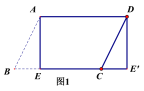
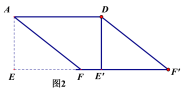
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com