
【题目】为鼓励居民节约用电,电力公司规定如下电费计算方法:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)若某用户某年1月交电费88元,那么该用户1月份用电多少度?
(2)若某用户某年2月份平均每度电费0.75元,那么该用户2月份用电多少度?应交电费多少元?
【答案】(1)128;(2)160度,120元.
【解析】
根据题意可知,电费计算方法为:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)如果用电100度,则需交电费100×0.6=60元,某用户交电费88元,![]() 则该用户用电超过100度,设该用户1月份用电
则该用户用电超过100度,设该用户1月份用电![]() 度,根据题意列出方程求解即可.
度,根据题意列出方程求解即可.
(2)由于此用户平均每度电费0.75元,所以其用电一定超过100度,所以可设此用户2月份共用电![]() 度,则其按每度0.6元费的为100度,按每度1元交费的为
度,则其按每度0.6元费的为100度,按每度1元交费的为![]() 度,由此可得等量关系式:
度,由此可得等量关系式:![]() 解此方程即得用电多少度,进而求出应交电费多少元.
解此方程即得用电多少度,进而求出应交电费多少元.
(1)如果用电100度,则需交电费100×0.6=60元,某用户交电费88元,![]() 则该用户用电超过100度,
则该用户用电超过100度,
设该用户1月份用电![]() 度,
度,
![]()
解得:![]()
答:设该用户1月份用电128度.
(2)设此用户2月份共用电![]() 度,
度,
![]()
解得:![]()
当![]() 时,
时,![]() 元.
元.
答:该用户2月份用电160度,应交电费,120元.


科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).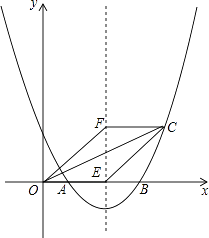
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.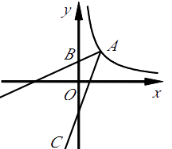
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③![]() ;④BD平分∠ADC;⑤∠BDC=
;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有_______个.
∠BAC.其中正确的结论有_______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( ) 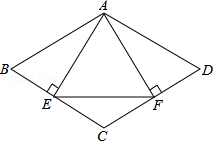
A.4 ![]()
B.3 ![]()
C.2 ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com