
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).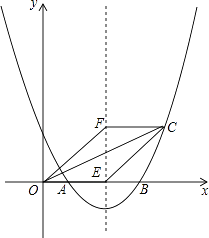
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:把点A(1,0)和B(4,0)代入y=ax2+bx+2得,
![]() ,
,
解得 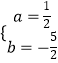 ,
,
所以,抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:方法一:
抛物线的对称轴为直线x= ![]() ,
,
∵四边形OECF是平行四边形,
∴点C的横坐标是 ![]() ×2=5,
×2=5,
∵点C在抛物线上,
∴y= ![]() ×52﹣
×52﹣ ![]() ×5+2=2,
×5+2=2,
∴点C的坐标为(5,2)
方法二:
∵FC∥x轴,∴当FC=OE时,四边形OECF是平行四边形.
设C(t, ![]() ),
),
∴F( ![]() ,
, ![]() +2),
+2),
∴t﹣ ![]() =
= ![]() ,
,
∴t=5,C(5,2)
(3)
解:方法一:
设OC与EF的交点为D,
∵点C的坐标为(5,2),
∴点D的坐标为( ![]() ,1),
,1),
①点O是直角顶点时,易得△OED∽△PEO,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PE= ![]() ,
,
所以,点P的坐标为( ![]() ,﹣
,﹣ ![]() );
);
②点C是直角顶点时,同理求出PF= ![]() ,
,
所以,PE= ![]() +2=
+2= ![]() ,
,
所以,点P的坐标为( ![]() ,
, ![]() );
);
③点P是直角顶点时,由勾股定理得,OC= ![]() =
= ![]() ,
,
∵PD是OC边上的中线,
∴PD= ![]() OC=
OC= ![]() ,
,
若点P在OC上方,则PE=PD+DE= ![]() +1,
+1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
若点P在OC的下方,则PE=PD﹣DE= ![]() ﹣1,
﹣1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形
),使△OCP是直角三角形
方法二:
∵点P在抛物线的对称轴上,设P( ![]() ,t),O(0,0),C(5,2),
,t),O(0,0),C(5,2),
∵△OCP是直角三角形,∴OC⊥OP,OC⊥PC,OP⊥PC,
①OC⊥OP,∴KOC×KOP=﹣1,∴ ![]() ,
,
∴t=﹣ ![]() ,∴P(
,∴P( ![]() ,﹣
,﹣ ![]() ),
),
②OC⊥PC,∴KOC×KPC=﹣1,∴ ![]() =﹣1,
=﹣1,
∴t= ![]() ,P(
,P( ![]() ,
, ![]() ),
),
③OP⊥PC,∴KOP×KPC=﹣1,∴ ![]() ,
,
∴4t2﹣8t﹣25=0,∴t= ![]() 或
或 ![]() ,
,
点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形.
),使△OCP是直角三角形.
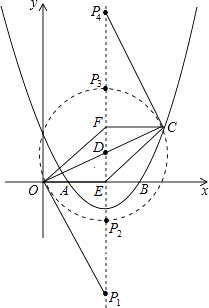
【解析】方法一:(1)把点A、B的坐标代入函数解析式,解方程组求出a、b的值,即可得解;(2)根据抛物线解析式求出对称轴,再根据平行四边形的对角线互相平分求出点C的横坐标,然后代入函数解析式计算求出纵坐标,即可得解;(3)设AC、EF的交点为D,根据点C的坐标写出点D的坐标,然后分①点O是直角顶点时,求出△OED和△PEO相似,根据相似三角形对应边成比例求出PE,然后写出点P的坐标即可;②点C是直角顶点时,同理求出PF,再求出PE,然后写出点P的坐标即可;③点P是直角顶点时,利用勾股定理列式求出OC,然后根据直角三角形斜边上的中线等于斜边的一半可得PD= ![]() OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
方法二:(1)略.(2)因为四边形OECF是平行四边形,且FC∥x轴,列出F,C的参数坐标,利用FC=OE,可求出C点坐标.(3)列出点P的参数坐标,分别列出O,C两点坐标,由于△OCP是直角三角形,所以分别讨论三种垂直的位置关系,利用斜率垂直公式,可求出三种情况下点P的坐标.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某学校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
![]() 求A种,B种树木每棵各多少元?
求A种,B种树木每棵各多少元?
![]() 因布局需要,购买A种树木的数量不少于B种树木数量的3倍
因布局需要,购买A种树木的数量不少于B种树木数量的3倍![]() 学校与中标公司签订的合同中规定:在市场价格不变的情况下
学校与中标公司签订的合同中规定:在市场价格不变的情况下![]() 不考虑其他因素
不考虑其他因素![]() ,实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,
,实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武警战士乘一冲锋舟从![]() 地逆流而上,前往
地逆流而上,前往![]() 地营救受困群众,途经
地营救受困群众,途经![]() 地时,由所携带的救生艇将
地时,由所携带的救生艇将![]() 地受困群众运回
地受困群众运回![]() 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到![]() 地接到群众后立刻返回
地接到群众后立刻返回![]() 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.

(1)请直接写出冲锋舟从![]() 地到
地到![]() 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将![]() 地群众安全送到
地群众安全送到![]() 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数关系式为
(分)之间的函数关系式为![]() ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离![]() 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年在中央“房子是用来住的,不是用来炒”的精神作用下,房子价格持续下跌.玲玲家买了一套新房准备装修,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费为4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑应选哪家公司?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
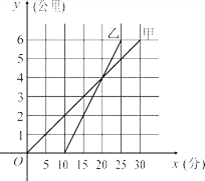
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
温度(℃)T | … | 15 | 17 | 20 | … |
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,电力公司规定如下电费计算方法:每月用电不超过100度,按每度0.6元计费;每月用电超过100度,超过部分按每度1元计费.
(1)若某用户某年1月交电费88元,那么该用户1月份用电多少度?
(2)若某用户某年2月份平均每度电费0.75元,那么该用户2月份用电多少度?应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com