
����Ŀ��ijУѧ�������������ѧ���������ѡ��һ�����£��Լס��ҡ���������ѡ�˽����˱��Ժ����ԣ����˵IJ��Գɼ����±���ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 75 | 80 | 90 |
���� | 93 | 70 | 68 |
����¼�ó���ѧУ��֯200��ѧ������ͶƱ�Ƽ��ķ�ʽ�������˽����������������˵�Ʊ�ʣ�û����Ȩ��ÿλͬѧֻ���Ƽ�1�ˣ�������ͳ��ͼ��ʾ��ÿ��һƱ��1�֣�
��1������ͳ��ͼ��![]() = , �ֱ����������������ĵ÷֣�
= , �ֱ����������������ĵ÷֣�
��2������ʵ����Ҫ��ѧУ�����ԡ����ԡ�������������÷ְ�4��3��3�ı���ȷ�����˳ɼ����÷�����߽���ѡ�У�ͨ������˵��������˭��ѡ�У�

���𰸡���1��a=25������������ĵ÷�50���֣�������������ĵ÷���80���֣�������������ĵ÷��ǣ� 70���֣���2�����ᱻѡ��.
�������������������1����1-40%-35%���ɵõ�a��ֵ���ٷֱ���200�������˵ĵ�Ʊ�ʣ����������������ĵ÷ָ��Ƕ��ټ��ɣ�
��2�����ݼ�Ȩƽ�����ļ��㷽����ʽ���㣬�ֱ�������˵ĵ÷ָ��Ƕ��٣�Ȼ��Ƚϴ�С���жϳ�������˭�ĵ÷�����ɣ�
�����������1��a%=1-40%-35%������a=25��
����������ĵ÷��ǣ�200��25%=50���֣���
����������ĵ÷��ǣ�200��40%=80���֣���
����������ĵ÷��ǣ�200��35%=70���֣���
��2���ijɼ��ǣ���75��4+93��3+50��3���£�4+3+3��=729��10=72.9���֣���
�ҵijɼ��ǣ���80��4+70��3+80��3���£�4+3+3��=770��10=77���֣���
���ijɼ��ǣ���90��4+68��3+70��3���£�4+3+3��=774��10=77.4���֣���
��77.4��77��72.9������ĵ÷���ߣ�����ѡ�У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
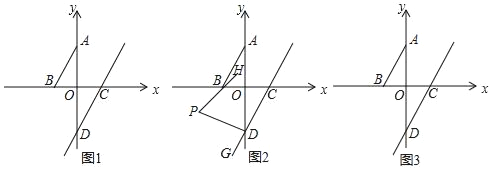
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߶�AB�������˵�ΪA��B�ֱ���y�������ᡢx�Ḻ�����ϣ�ֱ��CD�ֱ�x�������ᡢy�Ḻ�����ڵ�C��D����AB��CD��
��1����ͼ1������A��0��a���͵�B��b��0������������![]()
����ֱ��д��a��b��ֵ��a��_____��b��_____��
�������߶�ABƽ�ƣ�ʹB��Ķ�Ӧ��E��x�����Ϊ1��A��Ķ�Ӧ��F��y��ľ���Ϊ2����EF����������û�н��㣬��F�������Ϊ_____��
��2����G��CD�ӳ�����һ��DPƽ�֡�ADG��BHƽ�֡�ABO��BH�ķ����ӳ��߽�DP��P����ͼ2�������HPD�Ķ�����
��3������BAO��30�㣬��Q��x�ᣨ������B��C�����˶���AMƽ�֡�BAQ��QNƽ�֡�AQC������ͼ3����ӳ���BAM���NQC�����������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
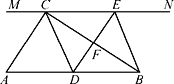
����Ŀ����ͼ����֪AB��CD������ͼ�й��ɼ�����ȥ�����1����2��������n����(����)


A. n��180�� B. 2n��180�� C. (n��1)��180�� D. (n��1)2��180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB= ![]() ��E��BC���е㣬AE��BD�ڵ�F����CF�ij��� ��
��E��BC���е㣬AE��BD�ڵ�F����CF�ij��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣���ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ֱ��ӳ�OA��OC����E��F��ʹAE=CF����������B��F��D��E���㣮

��1����֤����BAE�ա�BCF��
��2������ABC=50��������EBA= ��ʱ���ı���BFDE�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=a��x��h��2��4��a��0����x��ֱ���ԭ��O��A���㣬��A��x����������ϣ�����ΪD��ֱ��y= ![]() x����������B�㣬��B��BE��x�ύ��������һ��E�����Գ�����F��
x����������B�㣬��B��BE��x�ύ��������һ��E�����Գ�����F��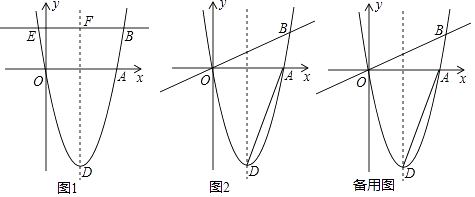
��1����DF=4aʱ����BE�ij���
��2����ͼ2����AD������AD�Ƶ�A��ת��ֱ��OB�ڵ�G����D�Ķ�Ӧ��ΪG����OG=2ʱ����a��ֵ��
��3���ڣ�2���������£���0��a��1ʱ����OBΪֱ����Բ��x���·��������ڵ�P�����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE.
��1����֤��CE��AD��
��2����DΪAB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬��A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=��B��AE=BE����D��AC���ϣ���1=��2��AE��BD�ཻ�ڵ�O��

��1����֤����AEC����BED��
��2������1=42��������BDE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com