
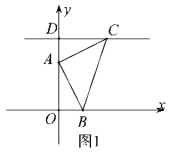
【题目】如图1,平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)![]() ;
;
(2)连接![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2,已知![]() ,
,![]() ,若
,若![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,则点
,则点![]() 坐标为 .
坐标为 .

【答案】(1)见解析;(2)![]() 为等腰直角三角形,见解析;(3)
为等腰直角三角形,见解析;(3)![]() 或
或![]()
【解析】
(1)根据点的坐标分别求出OD、CD,得到AD=OB,利用SAS定理证明△AOB≌△CDA;
(2)根据全等三角形的性质得到∠ABO=∠CAD,AC=AB,根据同角的余角相等得到∠BAC=90°,根据等腰直角三角形的定义解答;
(3)根据题意画出点M和点M′,过点P作x轴的平行线GH,作MG⊥GH于G,QH⊥GH于H,证明△GMP≌△HPQ,根据全等三角形的性质得到GM=PH=3,GP=HQ=2,得到点M坐标为(1,1),同理求出点M′坐标.
(1)∵C(2,3),![]() 轴于点
轴于点![]() ,
,
∴D(0,3)
∴OD=3,CD=2,
∵A(0,2),B(1,0),
∴OA=2,OB=1,
∴AD=1,
∴AD=OB,
在△AOB和△CDA中,
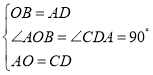 ,
,
∴△AOB≌△CDA(SAS);
(2)△ABC是等腰直角三角形,
理由如下:∵△AOB≌△CDA,
∴∠ABO=∠CAD,AC=AB,
∵∠ABO+∠BAO=90°,
∴∠CAD+∠BAO=90°,
∴∠BAC=90°,又AC=AB,
∴△ABC是等腰直角三角形;
(3)如图2,过点P作x轴的平行线GH,作MG⊥GH于G,QH⊥GH于H,
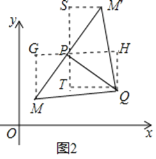
∵P(3,4),Q(6,2),
∴PH=3,QH=2,
∵△MPQ为等腰直角三角形,
∴∠MPQ=90°,PM=PQ,
∴∠MPG+∠HPQ=90°,
∵∠MPG+∠PMG=90°,
∴∠GMP=∠HPQ,
在△GMP和△HPQ中,
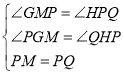 ,
,
∴△GMP≌△HPQ(AAS)
∴GM=PH=3,GP=HQ=2,
∴点M坐标为(1,1),
过点P作y轴的平行线ST,作M′S⊥ST于S,QT⊥ST于T,
同理可得,△M′ST≌△PTQ,
∴M′S=PT=2,SP=TQ=3,
∴点M′坐标为(5,7),
故答案为:(1,1)或(5,7).


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
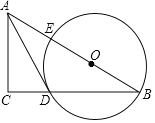
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
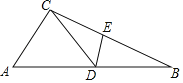
A.50°B.40°C.60°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,点C是OA的中点,过点C作CD⊥OA于C交一次函数图象于点D,P是OB上一动点,则PC+PD的最小值为( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开拓学生的视野,全面培养和提升学生的综合素质,让学生感受粤东古城潮州的悠久历史,某中学组织八年级师生共420人前往潮州开展研学活动.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车5辆,则空余15个座位;若租用A型车5辆,B型车3辆,则15人没座位.
(1)求A、B两种车型各有多少个座位?
(2)租车公司目前B型车只有6辆,若A型车租金为1800元/辆,B型车租金为2100元/辆,请你为学校设计使座位恰好坐满师生且租金最少的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
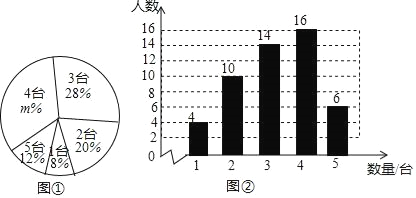
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com