练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ABC中，D为AB上一点，E为BC上一点，且AC＝CD＝BD＝BE，∠A＝40°，则∠CDE的度数为（　　）

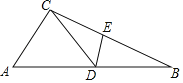
    A.50°B.40°C.60°D.80°

    【答案】C

    【解析】

    根据等腰三角形的性质推出∠A＝∠CDA＝40°，∠B＝∠DCB，∠BDE＝∠BED，根据三角形的外角性质求出∠B＝20°，由三角形的内角和定理求出∠BDE，根据平角的定义即可求出选项．

    ∵AC＝CD＝BD＝BE，∠A＝40°，

    ∴∠A＝∠CDA＝40°，∠B＝∠DCB，∠BDE＝∠BED，

    ∵∠B+∠DCB＝∠CDA＝40°，

    ∴∠B＝20°，

    ∵∠B+∠EDB+∠DEB＝180°，

    ∴∠BDE＝∠BED＝（180°﹣20°）＝80°，

    ∴∠CDE＝180°﹣∠CDA﹣∠EDB＝180°﹣40°﹣80°＝60°，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：弦切角：顶点在圆上，一边与圆相交，另一边和圆相切的角叫弦切角．

    问题情景：已知如图所示，直线是的切线，切点为，为的一条弦，为弧所对的圆周角．

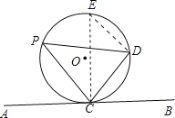
    （1）猜想：弦切角与之间的关系．试用转化的思想：即连接并延长交于点，连接，来论证你的猜想．

    （2）用自己的语言叙述你猜想得到的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知点D在线段AB的反向延长线上，过AC的中点F作线段GE交∠DAC的平分线于E，交BC于G，且AE∥BC．

    （1）求证：△ABC是等腰三角形；

    （2）若AE＝8，AB＝10，GC＝2BG，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：线段AB，BC．

    求作：平行四边形ABCD．

    以下是甲、乙两同学的作业．

    甲：

    ①以点C为圆心，AB长为半径作弧；

    ②以点A为圆心，BC长为半径作弧；

    ③两弧在BC上方交于点D，连接AD，CD．

    四边形ABCD即为所求平行四边形．（如图1）

    乙：

    ①连接AC，作线段AC的垂直平分线，交AC于点M；

    ②连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD．

    四边形ABCD即为所求平行四边形．（如图2）

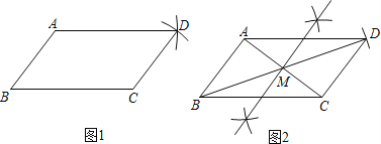
    老师说甲、乙同学的作图都正确，你更喜欢______的作法，他的作图依据是：______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】作图题．

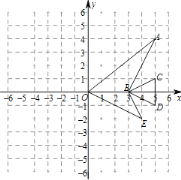
    小峰一边哼着歌“我是一条鱼，快乐的游来游去”，一边试着在平面直角坐标系中画出了一条鱼．如图，O（0，0），A（5，4），B（3，0），C（5，1），D（5，-1），E（4，-2）．

    （1）作“小鱼”关于原点O的对称图形，其中点O，A，B，C，D，E的对应点分别为O1，A1，B1，C1，D1，E1（不要求写作法）；

    （2）写出点A1，E1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

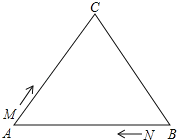
    【题目】如图，中，，现有两点、分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2 cm/s.当点N第一次到达B点时，、同时停止运动.

    （1）点、运动几秒时，、两点重合？

    （2）点、运动几秒时，可得到等边三角形？

    （3）当点、在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时、运动的时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

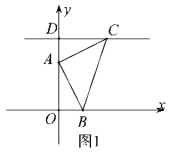
    【题目】如图1，平面直角坐标系中，，，，轴于点．

    （1）；

    （2）连接，判断的形状，并说明理由；

    （3）如图2，已知，，若是等腰直角三角形，且，则点坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形中，点，分别在边，上，，过点作，交的延长线与点．若一边的边长为2，则的周长为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中:①等腰三角形底边的中点到两腰的距离相等；②等腰三角形的高、中线、角平分线互相重合； ③若与成轴对称，则一定与全等；④有一个角是度的三角形是等边三角形；⑤等腰三角形的对称轴是顶角的平分线．正确命题的个数是（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案