
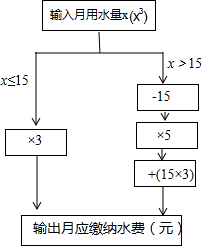
 ������С������������ˮ��˾�ľ�����ˮ�շѱ����ƶ�������ˮ�Ѽ������ת����ʾ��ͼ��
������С������������ˮ��˾�ľ�����ˮ�շѱ����ƶ�������ˮ�Ѽ������ת����ʾ��ͼ��| �û� | �Ŵ�ү | ������ | ������ | С���� |
| ���루m3�� | 8 | 15 | 18 | 25 |
| �����Ԫ�� | 24 | 45 | 60 | 95 |
���� ��1��������ˮ���Ķ��ٺ����ֲ�ͬ�ļ��㷽������ˮ�Ѽ��ɣ�
��2����15������ˮ�Ѽ��ϱ�15������IJ��ֵ�ˮ�Ѽ��ɣ�
��3��������ˮ��150Ԫ�������ˮ�����ɣ�
��� �⣺��1���Ŵ�үˮ�ѣ�8��3=24Ԫ��
������ˮ�ѣ�15��3=45Ԫ��
������ˮ�ѣ���18-15����5+15��3=60Ԫ��
С����ˮ�ѣ���25-15����5+15��3=95Ԫ��
��2���۲�ʾ��ͼ�ã���x��15ʱ����Ӧ����ˮ�ѣ�Ԫ����x�Ĵ���ʽ��ʾΪ15��3+5��x-15��=5x-30��
��3����150-15��3����5+15=105��5+15=21+15=36��m3����
��С���Ҹ�����ˮ36m3��
���� ���⿼�����д���ʽ��֪ʶ������Ĺؼ����ܹ�����ʾ��ͼ����˼��ʵ�ʱ�����һ���ֶ���ȡˮ�ѵ�֪ʶ���ѶȲ���


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2���� | B�� | 3���� | C�� | 4���� | D�� | 5���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
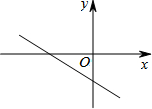 ��ͼ��ֱ��l��y=-$\frac{2}{3}$x-3��ֱ��y=a��aΪ�������Ľ����ڵ������ޣ���a��ȡֵ��Χ�ǣ�������
��ͼ��ֱ��l��y=-$\frac{2}{3}$x-3��ֱ��y=a��aΪ�������Ľ����ڵ������ޣ���a��ȡֵ��Χ�ǣ�������| A�� | a��0 | B�� | -3��a��0 | C�� | a��-3 | D�� | a��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
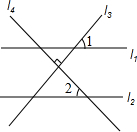 ��ͼ��ֱ��l1��l2��l3��l4����1=46�㣬��ô��2�Ķ���Ϊ��������
��ͼ��ֱ��l1��l2��l3��l4����1=46�㣬��ô��2�Ķ���Ϊ��������| A�� | 46�� | B�� | 44�� | C�� | 23�� | D�� | 22�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com