
分析 (2)根据给出的运算方法类比计算得出答案即可;
(3)(1)、(2)中的规律,拆成4个连续自然数的乘积得出答案即可.
解答 解:(2)4×5=$\frac{1}{3}$(4×5×6-3×4×5);
1×2+2×3+3×4+4×5…+(n-1)×n
=$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+$\frac{1}{3}$(3×4×5-2×3×4)+…+$\frac{1}{3}$[(n-1)n(n+1)-(n-2)(n-1)n]
=$\frac{1}{3}$[1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+(n-1)n(n+1)-(n-2)(n-1)n]
=$\frac{1}{3}$(n-1)n(n+1);
(3)问题解决:1×2×3+2×3×4+3×4×5+…+(n-2)(n-1)n
=$\frac{1}{4}$(1×2×3×4-0×1×2×3)+$\frac{1}{4}$(2×3×4×5-1×2×3×4)+$\frac{1}{4}$(3×4×5×6-2×3×4×5)+…+$\frac{1}{4}$[(n-2)(n-1)n(n+1)-(n-3)(n-2)(n-1)n]
=$\frac{1}{4}$[1×2×3×4-0×1×2×3+2×3×4×5-1×2×3×4+3×4×5×6-2×3×4×5+…+(n-2)(n-1)n(n+1)-(n-3)(n-2)(n-1)n]
=$\frac{1}{4}$(n-2)(n-1)n(n+1).
故答案为:4×5×6-3×4×5,(n-1)n(n+1)-(n-2)(n-1)n;(n-1)n(n+1)-(n-2)(n-1)n,=$\frac{1}{3}$[1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+(n-1)n(n+1)-(n-2)(n-1)n],$\frac{1}{3}$(n-1)n(n+1);$\frac{1}{4}$(n-2)(n-1)n(n+1).
点评 此题考查了有理数的混合运算,利用类比的思想与方法,得出运算的规律解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 12,15,20 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 0.3,0.4,0.5 | D. | 32,42,52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
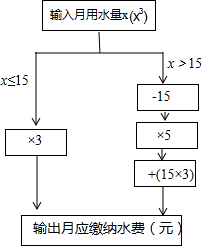 聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:| 用户 | 张大爷 | 刘奶奶 | 王阿姨 | 小明家 |
| 输入(m3) | 8 | 15 | 18 | 25 |
| 输出(元) | 24 | 45 | 60 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4x}{{x}^{2}-1}$ | B. | $\frac{1}{0.2{x}^{2}+1}$ | C. | $\frac{2}{x+2}$ | D. | $\frac{1}{11x+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com