【题目】已知，正方形ABCD的边长为6，菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上，AH=2．
（1）如图1，当DG=2，且点F在边BC上时.

求证：① △AHE≌△DGH；
② 菱形EFGH是正方形；
（2）如图2，当点F在正方形ABCD的外部时，连接CF.

① 探究：点F到直线CD的距离是否发生变化？并说明理由；
② 设DG=x，△FCG的面积为S，是否存在x的值，使得S=1，若存在，求出x的值；若不存在，请说明理由.

参考答案：

【答案】
（1）解：① 在正方形ABCD中，∠A=∠D=90°，

在菱形EFGH中，EH=HG，

又∵ AH=DG=2，

∴ △AHE≌△DGH.

② 由（1）知△AHE≌△DGH，

∴ ∠AHE=∠DGH．

∵ ∠DGH+∠DHG=90°，

∴ ∠DHG+∠AHE=90°，

∴ ∠GHE=90°，

∴ 菱形EFGH是正方形．


（2）解：① 点F到直线CD的距离没有发生变化，理由如下：

作FM⊥DC于M，连结GE. 如图，

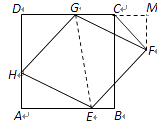
∵ AB∥CD, ∴∠AEG=∠MGE，

∵ HE∥GF, ∴∠HEG=∠FGE，

∴ ∠AEH=∠MGF．

在△AHE和△MFG中，∠A=∠M=90°，HE=FG，

∴ △AHE≌△MFG.

∴ FM=HA=2，即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2．

② 不存在.

∵ DG=x，∴ GC=6-x.

∴ S= S△FCG= ×2×(6-x)=6-x．

若S=S△FCG=1，∴ 由S△FCG=6-x，得x=5.

此时，在Rt△DGH中，HG= = ．

相应地，在Rt△AHE中，AE= ＞6，即点E已经不在边AB上．

故不可能有S=1


【解析】（1）①利用正方形的性质和菱形的性质易证出结论；
②由△AHE≌△DGH可得∠AHE=∠DGH，再由∠DGH+∠DHG=90°可得∠GHE=90°，再由正方形的判定定理可证出；
（2）①作FM⊥DC于M，连结GE. 证△AHE≌△MFG，则FM=HA=2，从而得出结论；
②先根据△FCG的面积求出x的值，在Rt△DGH中，利用勾股定理可求出HG的长，在Rt△AHE中，求AE的长，比较可得结论.

关闭