Question

【题目】如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论： ①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°﹣∠ABD；④BD平分∠ADC；⑤∠BDC= ∠BAC．
其中正确的结论有个．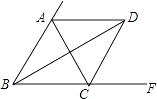

Answer 1

【答案】4
【解析】解：∵AD平分∠EAC， ∴∠EAC=2∠EAD，
∵∠EAC=∠ABC+∠ACB，∠ABC=∠ACB，
∴∠EAD=∠ABC，
∴AD∥BC，∴①正确；
∵AD∥BC，
∴∠ADB=∠DBC，
∵BD平分∠ABC，∠ABC=∠ACB，
∴∠ABC=∠ACB=2∠DBC，
∴∠ACB=2∠ADB，∴②正确；
在△ADC中，∠ADC+∠CAD+∠ACD=180°，
∵CD平分△ABC的外角∠ACF，
∴∠ACD=∠DCF，
∵AD∥BC，
∴∠ADC=∠DCF，∠ADB=∠DBC，∠CAD=∠ACB
∴∠ACD=∠ADC，∠CAD=∠ACB=∠ABC=2∠ABD，
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°，
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD，∴③正确；
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∵∠ADB=∠DBC，∠ADC=90°﹣ ∠ABC，
∴∠ADB不等于∠CDB，∴④错误；
∵∠ACF=2∠DCF，∠ACF=∠BAC+∠ABC，∠ABC=2∠DBC，∠DCF=∠DBC+∠BDC，
∴∠BAC=2∠BDC，∴⑤正确；
即正确的有4个，
所以答案是：4．
【考点精析】关于本题考查的平行线的判定和三角形的内角和外角，需要了解同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案．