
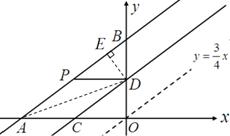
如图,直线 与
与 轴相交于点
轴相交于点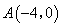 ,与
,与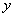 轴相交于点
轴相交于点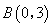 ,点
,点 从点
从点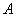 出发,以每秒
出发,以每秒 个单位长度的速度沿直线
个单位长度的速度沿直线 向点
向点 移动。同时,将直线
移动。同时,将直线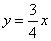 以每秒
以每秒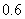 个单位长度的速度向上平移,交
个单位长度的速度向上平移,交 于点
于点 ,交
,交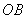 于点
于点 ,设运动时间为
,设运动时间为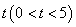 秒。
秒。
⑴证明:在运动过程中,四边形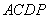 总是平行四边形;
总是平行四边形;
⑵当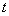 取何值时,四边形
取何值时,四边形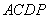 为菱形?请指出此时以点
为菱形?请指出此时以点 为圆心、
为圆心、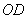 长为半径的圆与直线
长为半径的圆与直线 的位置关系并说明理由。
的位置关系并说明理由。
解:⑴∵直线 与
与 轴相交于点
轴相交于点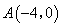 ,与
,与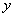 轴相交于点
轴相交于点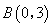
∴直线 的解析式为
的解析式为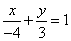 ,即
,即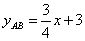
∵将直线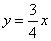 以每秒
以每秒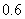 个单位长度的速度向上平移
个单位长度的速度向上平移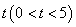 秒得到直线
秒得到直线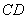
∴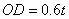 ,∴
,∴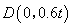 ,∴直线
,∴直线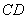 的解析式为
的解析式为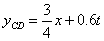
∵在直线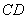 中,点
中,点 在
在 轴上,∴令
轴上,∴令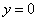 ,则
,则 ,∴
,∴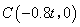 ,
,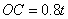
∴在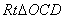 中,
中,
∵点 从点
从点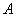 出发,以每秒
出发,以每秒 个单位长度的速度沿直线
个单位长度的速度沿直线 向点
向点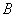 移动
移动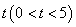 秒
秒
∴ ,∴
,∴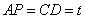 ,又∵
,又∵ ,∴
,∴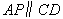 ,
,
∵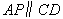 ,
,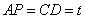 ,∴在运动过程中,四边形
,∴在运动过程中,四边形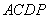 总是平行四边形;
总是平行四边形;
⑵欲使四边形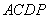 为菱形,只需在
为菱形,只需在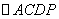 中满足条件
中满足条件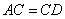 ,即
,即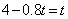 ,解得
,解得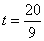
∴当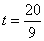 时,四边形
时,四边形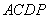 为菱形;
为菱形;
此时以点 为圆心、
为圆心、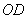 长为半径的圆与直线
长为半径的圆与直线 相切,理由如下:
相切,理由如下:
∵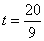 ,∴
,∴ ,∴
,∴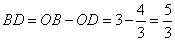
∵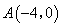 ,
,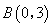 ,∴
,∴ ,
,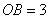 ,∴在
,∴在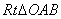 中,
中,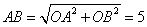
过点 作
作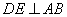 于点
于点 ,则
,则
∵在 和
和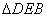 中,
中,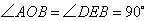 且
且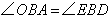 ,∴
,∴ ∽
∽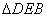
∴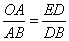 ,即
,即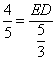 ,∴
,∴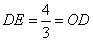 ,∴点
,∴点 到直线
到直线 的距离等于
的距离等于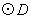 的半径
的半径
∴以点 为圆心、
为圆心、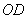 长为半径的圆与直线
长为半径的圆与直线 相切。
相切。
另解:(在证明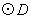 与直线
与直线 相切时,也可利用等积法求得点
相切时,也可利用等积法求得点 到直线
到直线 的距离。)
的距离。)
设点 到直线
到直线 的距离为
的距离为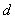 ,则
,则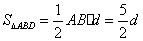 ,连结
,连结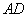 ,
,
∵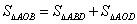 且
且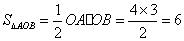 、
、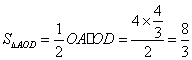
∴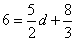 ,解得
,解得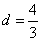 ,∴点
,∴点 到直线
到直线 的距离与
的距离与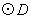 的半径相等,即
的半径相等,即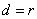
∴以点 为圆心、
为圆心、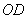 长为半径的
长为半径的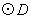 与直线
与直线 相切。
相切。
再解:(巧用“菱形对角线的性质”和“角平分线性质定理”)
连结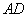 ,则
,则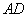 是菱形
是菱形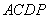 的对角线,∴
的对角线,∴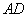 平分
平分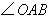
∵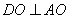 ,∴
,∴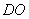 是点
是点 到直线
到直线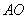 的距离,
的距离,
∴点 到直线
到直线 的距离=点
的距离=点 到直线
到直线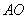 的距离
的距离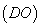
∴以点 为圆心、
为圆心、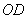 长为半径的圆与直线
长为半径的圆与直线 相切。
相切。


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
阅读理解:如图3,在平面内选一定点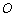 ,引一条有方向的射线
,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点M的位置可由
,再选定一个单位长度,那么平面上任一点M的位置可由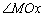 的度数
的度数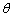 与
与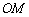 的长度m确定,有序数对(
的长度m确定,有序数对(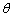 ,m)称为
,m)称为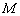 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图4的极坐标系下,如果正六边形的边长为2,有一边OA在射线 上,则正六边形的顶点C的极坐标应记为
上,则正六边形的顶点C的极坐标应记为
A.(60°,4) B.(45°,4) C.(60°,2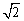 ) D.(50°,2
) D.(50°,2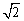 )
)
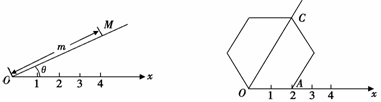
图3  图4
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
在“黄袍山国家油茶产业示范园”建设中,某农户计划购买甲、乙两种油茶树苗共1000株.已知乙种树苗比甲种树苗每株贵3元,且用100元钱购买甲种树苗的株数与用160元钱购买乙种树苗的株数刚好相同.
(1)求甲、乙两种油茶树苗每株的价格;
(2)如果购买两种树苗共用5600元,那么甲、乙两种树苗各买了多少株?
(3)调查统计得,甲、乙两种树苗的成活率分别为90%,95%.要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
为了了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了我市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出)。
我市若干天空气质量情况条形统计图 我市若干天空气质量情况扇形统计图
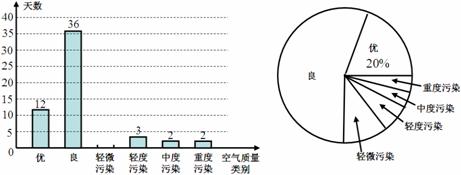
请你根据图中提供的信息,解答下列问题:
⑴请补全条形统计图;
⑵求扇形统计图中表示“优”的扇形的圆心角度数;
⑶请估计我市这一年(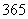 天)达到“优”和“良”的总天数。
天)达到“优”和“良”的总天数。
查看答案和解析>>
科目:初中数学 来源: 题型:
如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是().
(A) y=x2-1; (B) y=x2+1; (C) y=(x-1)2; (D) y=(x+1)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com