
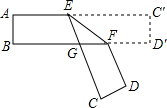
 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行线的性质由AC′∥BD′,得到∠C′EF=∠EFB=32°;根据折叠的性质得∠C′EF=∠FEC,则∠C′EC=2×32°=64°,利用平角的定义得到∠AEC=180°-64°=116°;再根据折叠性质有∠BFD=∠EFD′,利用平角的定义得到∠BFD=∠EFD′-∠BFE=180°-2∠EFB=180°-64°=116°;根据平行线性质可得∠BGE=∠C′EC=2×32°.
解答 解:∵AC′∥BD′,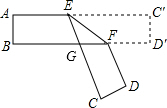
∴∠C′EF=∠EFB=32°,所以(1)正确;
∵∠C′EF=∠FEC,
∴∠C′EC=2×32°=64°,
∴∠AEC=180°-64°=116°,所以(2)正确;
∴∠BFD=∠EFD′-∠BFE=180°-2∠EFB=180°-64°=116°,所以(4)正确;
∠BGE=∠C′EC=2×32°=64°,所以(3)正确.
故选D.
点评 本题考查的是平行线的性质及翻折变换的性质,熟知图形翻折不变性的性质是解答此题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
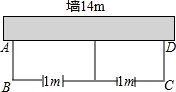 如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.
如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=±2 | B. | $x=±\frac{1}{2}$ | C. | x=±2或x=±$\frac{1}{2}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com