
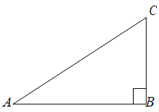
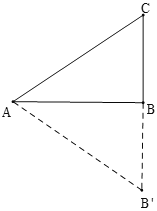
【题目】如图,有一直角三角形纸片ABC,∠B=90°,AB=8,BC=6,AC=10.
(1)将三角形纸片ABC沿着射线AB方向平移AB长度得到△BDE(点B、C分别与点 D、E对应),在图中画出△BDE,求出△ABC在平移过程中扫过的图形的面积;
(2)三角形纸片ABC是由一张纸对折后(折痕两旁完全重合)得到的,展开这张折纸后就可以得到原始的图形,那么原始图形的周长为_______.
【答案】(1)画图见解析;△ABC扫过的图形的面积为72;(2)28或32或36.
【解析】
(1)根据平移的性质可知点A与点B重合,BD=AB,DE=BC,DE⊥BD,据此画出图形即可,由图形可知△ABC扫过的图形的面积为梯形ADEC的面积,利用梯形面积公式即可得答案;
(2)分对称轴为AC、BC、AB三种情况讨论,根据轴对称的性质即可求出原始图形的周长.
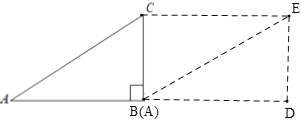
(1)∵将三角形纸片ABC沿着射线AB方向平移AB长度得到△BDE,
∴A与点B重合,BD=AB,DE=BC,DE⊥BD,CE=AB,
∴延长AB到D,使BD=AB,过D作DE⊥BD,且使DE=BC,连接BE,
∴△BDE即为所求,
∵△ABC在平移过程中扫过的图形为梯形ADEC,CE=AB=8,
∴△ABC扫过的图形图形面积为![]() (AD+CE)·BC=
(AD+CE)·BC=![]() (16+8)×6=72,
(16+8)×6=72,
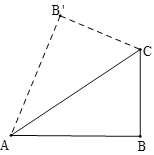
(2)①如图,当AC为对称轴时,
∵三角形ABC与三角形AB′C关于AC对称,
∴AB′=AB=8,B′C=BC=6,
∴原始图形的周长为2(AB+BC)=2×(8+6)=28,
②如图,当BC为对称轴时,
∴AC=B′C=10,AB=AB′=8,
∴原始图形的周长为2(AB+AC)=2×(8+10)=36,
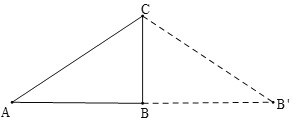
③如图,当AB为对称轴时,
∴AC=AB′=10,BB′=BC=6,
∴原始图形的周长为2(AC+BC)=2×(10+6)=32,
综上所述:原始图形的周长为28或32或36.


科目:初中数学 来源: 题型:
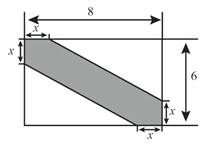
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励学生积极参加体育锻炼,某学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生所穿运动鞋的号码,绘制了如下的统计图①和图②(不完整).请根据相关信息,解答下列问题:
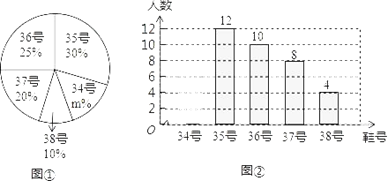
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)请补全条形统计图,并求本次调查样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买400双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E,若BD=4,DE=9,则线段CE的长为( )
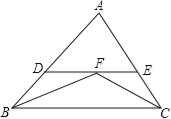
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
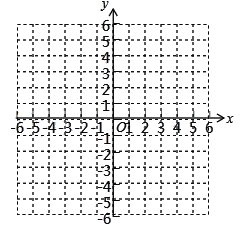
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出三角形ABC;
(2)若三角形ABC内有一点P(![]() ,
,![]() )经平移后对应点为P1(
)经平移后对应点为P1(![]() ,
,![]() ),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
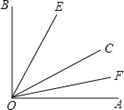
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=![]() ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA”,且∠AOB=
∠COA”,且∠AOB=![]() ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料![]() :我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为
:我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为![]() ,
,![]() ,
,![]() ,我们把它的面积记为
,我们把它的面积记为![]() ,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:
,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:![]() (其中
(其中![]() )
)
材料2:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即![]() .配方法是中学数学的重要方法,用配方法可求最最大(小)值.
.配方法是中学数学的重要方法,用配方法可求最最大(小)值.
例如:求![]() 的最小值.
的最小值.
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]() 取得最小值
取得最小值![]() ,
,
请你运用材料提供的方法,解答以下问题:
(1)若三角形的三边长分别为![]() ,
,![]() ,
,![]() ,求该三角形的面积;
,求该三角形的面积;
(2)小新手里有一根长![]() 米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为
米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为![]() 米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com