
【题目】为鼓励学生积极参加体育锻炼,某学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生所穿运动鞋的号码,绘制了如下的统计图①和图②(不完整).请根据相关信息,解答下列问题:
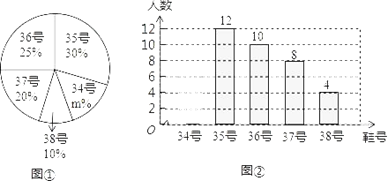
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)请补全条形统计图,并求本次调查样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买400双运动鞋,建议购买35号运动鞋多少双?
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费每户每月用水量如果未超过20t,按每吨2.5元收费.如果超过20t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为xt,应收水费为y元.
(1)分别写出每月用水量未超过20t和超过20t时y与x间的关系式.
(2)若该城市某户4月份水费平均为每吨2.8元,求该户4月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
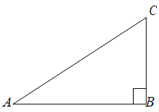
【题目】如图,有一直角三角形纸片ABC,∠B=90°,AB=8,BC=6,AC=10.
(1)将三角形纸片ABC沿着射线AB方向平移AB长度得到△BDE(点B、C分别与点 D、E对应),在图中画出△BDE,求出△ABC在平移过程中扫过的图形的面积;
(2)三角形纸片ABC是由一张纸对折后(折痕两旁完全重合)得到的,展开这张折纸后就可以得到原始的图形,那么原始图形的周长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
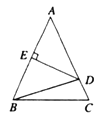
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于点D、E,若△ABC和△BDC 的周长分别为40cm和25cm ,则BC=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在用黑色围棋进行摆放图案的游戏中,一同学摆放了如下图案,请根据图中信息完成下列的问题:
 ...
...
(1)填写下表:
图形编号 | ① | ② | ③ | … | … |
图中棋子的总数 | ________ | ________ | ________ | … | … |
(2)第10个图形中棋子为________颗围棋;
(3)该同学如果继续摆放下去,那么第![]() 个图案要用________颗围棋;
个图案要用________颗围棋;
查看答案和解析>>
科目:初中数学 来源: 题型:
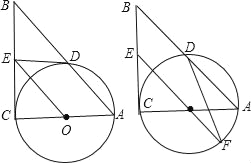
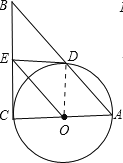
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
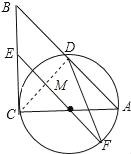
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,
∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()
【题型】解答题
【结束】
23
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com