Question

【题目】如图，已知点A（2，2）关于直线y=k（k>0）的对称点恰好落在x轴的正半轴上，则k的值是_____．

Answer 1

【答案】

【解析】分析：

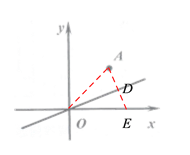
如图，设点A关于直线y=kx的对称点为点E，连接OA，连接AE交直线y=kx于点D，由已知条件易得OA=，由轴对称的性质可得OE=AE=，由此可得点E的坐标为，根据线段的中点坐标公式可得点D的坐标，将点D的坐标代入直线y=kx即可求得k的值.

详解：

如图，设点A关于直线y=kx的对称点为点E，连接OA，连接AE交直线y=kx于点D，

∵点A的坐标为（2，2），

∴OA=，

∵点E是点A关于直线y=kx的对称点，且点E在x轴的正半轴上，

∴OE=OA=，

∴点E的坐标为，

∵由折叠的性质可知：点D是线段AE的中点，

∴点D在坐标为：，

将点D在坐标为：代入y=kx得：

，解得：.

故答案为：.