
【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积为______。

【答案】36
【解析】
连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
连接AC,如图所示:
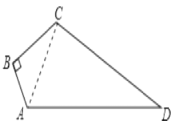
∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC=![]() =5,
=5,
又∵CD=12,AD=13,
∴AD![]() =13
=13![]() =169,CD
=169,CD![]() +AC
+AC![]() =12
=12![]() +5
+5![]() =144+25=169,
=144+25=169,
∴CD![]() +AC
+AC![]() =AD
=AD![]() ,
,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×12=36,
×5×12=36,
故四边形ABCD的面积是36


科目:初中数学 来源: 题型:
【题目】在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.记,![]()
![]() ,
,![]() .
.
同学们,通过以上材料的阅读,请回答下列问题:
(1)计算(填写最后的结果)
![]() =__________;
=__________;![]() ____________.
____________.
(2)2+4+6+8+10用求和公式符号可表示为__________.
(3)化简:![]()
(4)若对于任意x都存在![]() ,请求代数式
,请求代数式![]() b-ab的值.
b-ab的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐橘子,以每筐20千克为标准,超过或不足的部分分别用正数或负数来表示,记录如下:
与标准重量的差(单位:千克) | -2 | -1.5 | -1 | 0 | 1 | 1.5 |
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)求最重的一筐比最轻的一筐重多少?
(2)求20筐橘子的总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队新兵入伍时,对新兵进行“引体向上”测试,以50次为标准,超过50次用正数表示,不足50次用负数表示,第二小队的10名新兵的成绩如下表:
3 |
| 0 | 8 | 7 |
| 10 | 1 |
| 5 |
(1)求第二小队的总成绩;
(2)求第二小队的平均成绩。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式![]() x2y4的次数为c.
x2y4的次数为c.
![]()
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,边长为8的正方形OABC的两边在坐标轴上(如图).

(1)求点A,B,C的坐标.
(2)经过A,C两点的直线l上有一点P,点D(0,6)在y轴正半轴上,连PD,PB(如图1),若PB2﹣PD2=24,求四边形PBCD的面积.
(3)若点E(0,1),点N(2,0)(如图2),经过(2)问中的点P有一条平行于y轴的直线m,在直线m上是否存在一点M,使得△MNE为直角三角形?若存在,求M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于南北延伸的海岸线上,东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P,各自沿固定方向航行,“远洋”号每小时航行12n mile,“长峰”号每小时航行16n mile,它们离开港东口1小时后,分别到达A,B两个位置,且AB=20n mile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在RtΔABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连接OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连接DE.
(1)如图一,当点O在RtΔABC内部时.

①按题意补全图形;
②猜想DE与BC的数量关系,并证明.
(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com