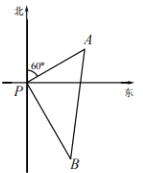
【题目】如图，某港口P位于南北延伸的海岸线上，东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P，各自沿固定方向航行，“远洋”号每小时航行12n mile，“长峰”号每小时航行16n mile，它们离开港东口1小时后，分别到达A，B两个位置，且AB=20n mile，已知“远洋”号沿着北偏东60°方向航行，那么“长峰”号航行的方向是________.
应用题天天练四川大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，已知数轴上原点为0，点B表示的数为2，A在B的右边，且A与B的距离为5，,动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时动点Q从点A出发，以每秒4个单位长度的速度向左匀速运动。设运动时间为t秒(t>0).
（1）写出数轴上点A表示的数 ，点P表示的数 （用含t的代数式表示），点Q表示的数（用含t的代数式表示）；
（2）问点P与点Q何时到点O的距离相等？
（3）若点D是数轴上一点，点D表示的数是x，是否存在x，使得
？如果存在，请直接写出x的值；如果不存在，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算（写出计算过程）
（1）(-35) + 18 + (-5) + (+22)
（2）
（3）
（4）
（5）
（6）9＋5×(－3)－(－2)2÷4
（7）(-22)×(-3)2+(-32)÷4;
（8）﹣32+1÷4×
﹣|﹣1|×（﹣0.5）2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算题
（1）30-（-12）-（-25）-18+（-10）
（2） (－
＋
－
)
．
（3）-52÷(-3)2×(-5)3÷[-(-5)2]
（4）（－2
＋3
）－（2－
）＋6
（5）
－[(－)＋4]－
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．
根据以上信息解决下列问题：
（1）
，
；
（2）扇形统计图中机器人项目所对应扇形的圆心角度数为 
；
（3）从选航模项目的
名学生中随机选取
名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的
名学生中恰好有
名男生、
名女生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.
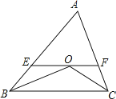
(1) 结合图形，请你写出你认为正确的结论；
(2) 过O作EF∥BC交AB于E，交AC于F. 请你写出图中所有等腰三角形，并探究EF、BE、FC之间的关系；
(3) 若AB≠AC，其他条件不变，图中还有等腰三角形吗？若有，请写出所有的等腰三角形，若没有，请说明理由；线段EF、BE、FC之间，上面探究的结论是否还成立？
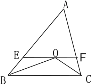
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，∠ACB=90°，∠BAC=30°，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s的速度向右移动．
（1）当点B于点O重合的时候，求三角板运动的时间；
（2）三角板继续向右运动，当B点和E点重合时，AC与半圆相切于点F，连接EF，如图2所示．
①求证：EF平分∠AEC；
②求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），将线段AB先向上平移2个单位长度，再向右平移1个单位长度，得到线段CD，连接AC，BD，构成平行四边形ABDC．
（1）请写出点C的坐标为 ，点D的坐标为 ，S四边形ABDC ；
（2）点Q在y轴上，且S△QAB＝S四边形ABDC，求出点Q的坐标；
（3）如图（2），点P是线段BD上任意一个点（不与B、D重合），连接PC、PO，试探索∠DCP、∠CPO、∠BOP之间的关系，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
