
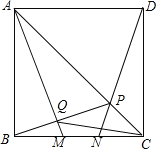
【题目】如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是_____.
【答案】![]()
【解析】
首先证明点Q在以AB为直径的圆上运动,连接OC与 O交于点Q′,此时CQ′最小,根据勾股定理即可计算.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ACB=∠ACD=45°
在△ABM和△DCN中,
 ,
,
∴△ABM≌△DCN,
∴∠BAM=∠CDN,
在△CPB和△CPD中,
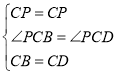 ,
,
∴△CPD≌△CPB,
∴∠CDP=∠CBP=∠BAM,
∵∠CBP+∠ABP=90°,
∴∠BAM+∠ABP=90°,
∴∠AQB=90°,
∴点Q在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于点Q′,此时CQ′最小,
∴CQ′=OC﹣OQ′=![]() .
.
故答案为![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上一动点,作
上一动点,作![]() ⊥
⊥![]() ,垂足
,垂足![]() 在边
在边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆,交射线
为半径画圆,交射线![]() 于点
于点![]() .
.
(1)当圆![]() 过点
过点![]() 时,求圆
时,求圆![]() 的半径;
的半径;
(2)分别联结![]() 和
和![]() ,当
,当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() 与圆
与圆![]() 相交,试求圆
相交,试求圆![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)将劣弧![]() 沿直线
沿直线![]() 翻折交
翻折交![]() 于点
于点![]() ,试通过计算说明线段
,试通过计算说明线段![]() 和
和![]() 的比值为定值,并求出次定值.
的比值为定值,并求出次定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
(1)求n的值.
(2)这个样本数据的中位数落在第几组?
(3)若测试九年级男生“排球30秒”对墙垫球个数不低于10个为合格,根据统计结果,估计该校九年级450名男同学成绩合格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
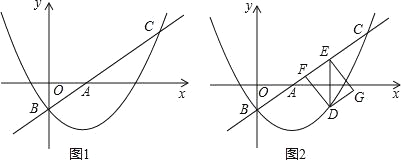
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
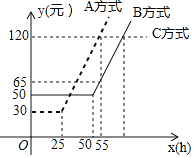
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①![]() ; ②
; ②![]() ; ③
; ③![]() ;④CE2=CD×BC; ⑤BE2=AE×BC
;④CE2=CD×BC; ⑤BE2=AE×BC

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
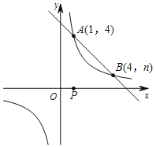
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com