
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上一动点,作
上一动点,作![]() ⊥
⊥![]() ,垂足
,垂足![]() 在边
在边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆,交射线
为半径画圆,交射线![]() 于点
于点![]() .
.
(1)当圆![]() 过点
过点![]() 时,求圆
时,求圆![]() 的半径;
的半径;
(2)分别联结![]() 和
和![]() ,当
,当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() 与圆
与圆![]() 相交,试求圆
相交,试求圆![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)将劣弧![]() 沿直线
沿直线![]() 翻折交
翻折交![]() 于点
于点![]() ,试通过计算说明线段
,试通过计算说明线段![]() 和
和![]() 的比值为定值,并求出次定值.
的比值为定值,并求出次定值.

【答案】(1)x=3 (2)![]() (3)
(3)![]()
【解析】
(1)作AM⊥BC、连接AP,由等腰梯形性质知BM=4、AM=3,据此知tanB=tanC=![]() ,从而可设PH=3k,则CH=4k、PC=5k,再表示出PA的长,根据PA=PH建立关于k的方程,解之可得;
,从而可设PH=3k,则CH=4k、PC=5k,再表示出PA的长,根据PA=PH建立关于k的方程,解之可得;
(2)由PH=PE=3k、CH=4k、PC=5k及BC=9知BE=98k,由△ABE∽△CEH得![]() ,据此求得k的值,从而得出圆P的半径,再根据两圆间的位置关系求解可得;
,据此求得k的值,从而得出圆P的半径,再根据两圆间的位置关系求解可得;
(3)在圆P上取点F关于EH的对称点G,连接EG,作PQ⊥EG、HN⊥BC,先证△EPQ≌△PHN得EQ=PN,由PH=3k、HC=4k、PC=5k知sinC=![]() 、cosC=
、cosC=![]() ,据此得出NC=
,据此得出NC=![]() k、HN=
k、HN=![]() k及PN=PCNC=
k及PN=PCNC=![]() k,继而表示出EF、EH的长,从而出答案.
k,继而表示出EF、EH的长,从而出答案.
(1)作AM⊥BC于点M,连接AP,如图1,

∵梯形ABCD中,AD//BC,且AB=DC=5、AD=1、BC=9,
∴BM=4、AM=3,
∴tanB=tanC=![]() ,
,
∵PH⊥DC,
∴设PH=3k,则CH=4k、PC=5k,
∵BC=9,
∴PM=BCBMPC=55k,
∴AP![]() =AM
=AM![]() +PM
+PM![]() =9+(55k)
=9+(55k) ![]() ,
,
∵PA=PH,
∴9+(55k) ![]() =9k
=9k![]() ,
,
解得:k=1或k=![]() ,
,
当k=![]() 时,CP=5k=
时,CP=5k=![]() >9,舍去;
>9,舍去;
∴k=1,
则圆P的半径为3.
(2)如图2,

由(1)知,PH=PE=3k、CH=4k、PC=5k,
∵BC=9,
∴BE=BCPEPC=98k,
∵△ABE∽△CEH,
∴![]() ,即
,即![]() ,
,
解得:k=![]() ,
,
则PH=![]() ,即圆P的半径为
,即圆P的半径为![]() ,
,
∵圆B与圆P相交,且BE=98k=![]() ,
,
∴![]() <r<
<r<![]() ;
;
(3)在圆P上取点F关于EH的对称点G,连接EG,作PQ⊥EG于G,HN⊥BC于N,

则EG=EF、∠1=∠3、EQ=QG、EF=EG=2EQ,
∴∠GEP=2∠1,
∵PE=PH,
∴∠1=∠2,
∴∠4=∠1+∠2=2∠1,
∴∠GEP=∠4,
∴△EPQ≌△PHN,
∴EQ=PN,
由(1)知PH=3k、HC=4k、PC=5k,
∴sinC=![]() 、cosC=
、cosC=![]() ,
,
∴NC=![]() k、HN=
k、HN=![]() k,
k,
∴PN=PCNC=![]() k,
k,
∴EF=EG=2EQ=2PN=![]() k,EH=
k,EH=![]() ,
,
∴![]() ,
,
故线段EH和EF的比值为定值.


科目:初中数学 来源: 题型:
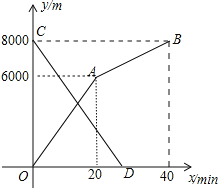
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y与销售单价x之间的关系可以近似地看作一次函数:y=﹣5x+150,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元;
(2)该文具店这种笔记本每月获得利润为W元,求每月获得的利润W元与销售单价x之间的函数关系式,并写出自变量的取值范围;
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是 ( )
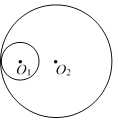
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为20万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破40辆.
(1)设当月该型号汽车的销售量为![]() 辆(
辆(![]() ,且
,且![]() 为正整数),实际进价为
为正整数),实际进价为![]() 万元/辆,求
万元/辆,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该型号汽车的销售价为22万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车.他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是_____.
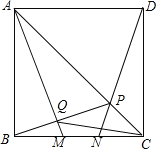
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com