
【题目】如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= . 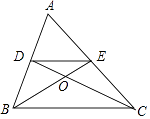
【答案】2:1
【解析】解:∵在△ABC中,两条中线BE、CD相交于点O,
∴DE为中位线,
∴DE∥BC,DE= ![]() BC,
BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴S△ADE:S△ABC=1:4,S△DOE:S△COB=1:4,
∵OD:OC=1:2,
∴S△DOE:S△COE=1:2,S△DOB:S△COB=1:2,
∴S△COE= ![]() S四边形DBCE,
S四边形DBCE,
则S△ADE:S△COE=2:1.
所以答案是:2:1
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E 在 AD 的延长线上,下列条件中能判断 AB∥CD 的是( )

A. ∠1=∠4B. ∠2=∠3C. ∠C=∠CDED. ∠C+∠CDA=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于D,点E为AC上一动点,过点E作EF⊥AB于F,连接DE.
(1)若∠1=∠2,求证:DE∥BC;
(2)在点E运动过程中,直线DE与直线BC交于点M,若∠DCB=α,∠M=β,则∠FED的度为 (用含α,β的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A坐标为(a,0),点B坐标为(b,2),点C坐标为(c,m),其中a、b、c满足方程组![]() .
.

(1)若a=2,则三角形AOB的面积为 ;
(2)若点B到y轴的距离是点C到y轴距离的2倍,求a的值;
(3)连接AB、AC、BC,若三角形ABC的面积小于等于9,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有红、黑、白三种球共![]() 个,他们除了颜色外其余完全一样. 已知黑球是白球的
个,他们除了颜色外其余完全一样. 已知黑球是白球的![]() 倍少
倍少![]() 个,将球充分搅匀后,随机摸出一球是红球的概率是
个,将球充分搅匀后,随机摸出一球是红球的概率是![]()
(1)这三种球各有多少个?
(2)随机摸出一球是白球的概率是多少?
(3)若从袋子中拿出![]() 个球(没有红球)后,随机摸一次摸到红球的概率是多少?
个球(没有红球)后,随机摸一次摸到红球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元.两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款.某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.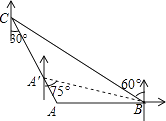
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com