
【题目】在一个不透明的袋子中装有红、黑、白三种球共![]() 个,他们除了颜色外其余完全一样. 已知黑球是白球的
个,他们除了颜色外其余完全一样. 已知黑球是白球的![]() 倍少
倍少![]() 个,将球充分搅匀后,随机摸出一球是红球的概率是
个,将球充分搅匀后,随机摸出一球是红球的概率是![]()
(1)这三种球各有多少个?
(2)随机摸出一球是白球的概率是多少?
(3)若从袋子中拿出![]() 个球(没有红球)后,随机摸一次摸到红球的概率是多少?
个球(没有红球)后,随机摸一次摸到红球的概率是多少?
【答案】(1)红球有30,黑球45,白球有25;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)根据红、黑、白三种颜色球共有的个数乘以红球的概率求出红球的数量,再设白球有x个,得出黑球有(2x-5)个,根据题意列出方程,求出白球的个数,即可解答;
(2)由(1)可知白球的数量,再除以总的球数即可;
(3)先求出取走10个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)根据题意得:
红球有100×![]() =30,
=30,
设白球有x个,则黑球有(2x-5)个,
根据题意得x+2x-5=100-30
解得x=25.
∴黑球2×25-5=45,
答:红球有30,黑球45,白球有25.
(2)有(1)可知白球有25个,
所以摸出一个球是白球的概率P=![]() ;
;
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率![]() ;
;


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
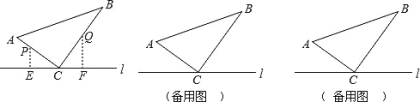
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.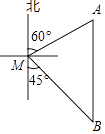
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发的960件新产品必须加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等,而且乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导.
(1)甲、乙两个工厂每天各能加工多少件产品?
(2)该公司要选择既省时又省钱的工厂加工产品,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,有望加工这批产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )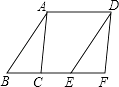
A.18cm2
B.21cm2
C.27cm2
D.30cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com