
【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.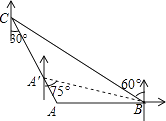
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
【答案】
(1)解:如图所示: 
延长BA,过点C作CD⊥BA延长线与点D,
由题意可得:∠CBD=30°,BC=120海里,
则DC=60海里,
故cos30°= ![]() =
= ![]() =
= ![]() ,
,
解得:AC=40 ![]() ,
,
答:点A到岛礁C的距离为40 ![]() 海里;
海里;
(2)解:如图所示:过点A′作A′N⊥BC于点N,
可得∠1=30°,∠BA′A=45°,
则∠2=15°,即A′B平分∠CBA,
设AA′=x,则A′E= ![]() x,
x,
故CA′=2A′N=2× ![]() x=
x= ![]() x,
x,
∵ ![]() x+x=40
x+x=40 ![]() ,
,
∴解得:x=60﹣20( ![]() ,
,
答:此时“中国海监50”的航行距离为(60﹣20 ![]() )海里
)海里
【解析】(1)根据题意得出:∠CBD=30°,BC=120海里,利用cos30°= ![]() ,进而求出答案;(2) 根据题意结合已知得出当点B在A′的南偏东75°的方向上,则A′B平分∠CBA,进而得出等式求出答案。
,进而求出答案;(2) 根据题意结合已知得出当点B在A′的南偏东75°的方向上,则A′B平分∠CBA,进而得出等式求出答案。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某公司开发的960件新产品必须加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等,而且乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导.
(1)甲、乙两个工厂每天各能加工多少件产品?
(2)该公司要选择既省时又省钱的工厂加工产品,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,有望加工这批产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为零.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
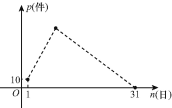
(1)写出p关于n的函数关系式 .(注明n的取值范围)
(2)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )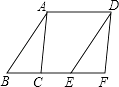
A.18cm2
B.21cm2
C.27cm2
D.30cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com