
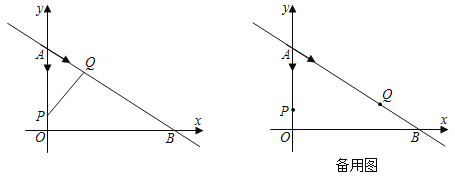
【题目】如图在平面直角坐标系xOy中,直线y=﹣![]() x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
(1)如果点Q的速度为每秒![]() 个单位长度,那么当t=5时,求证:△APQ∽△ABO;
个单位长度,那么当t=5时,求证:△APQ∽△ABO;
(2)如果点Q的速度为每秒2个单位长度,那么多少秒时,△APQ的面积为16?
(3)若点H为平面内任意一点,当t=4时,以点A,P,H,Q四点为顶点的四边形是矩形,请直接写出此时点H的坐标.
【答案】(1)证明见解析;(2)2![]() 秒时,△APQ的面积为16;(3)点H的坐标为:(
秒时,△APQ的面积为16;(3)点H的坐标为:(![]() ,6),(﹣
,6),(﹣![]() ,4).
,4).
【解析】
(1)根据已知得:直线与x、y轴的交点B(8,0)、A(0,6),AP=5,AQ=3,对应边成比例且夹角相等即可证明;
(2)作QE⊥y轴于点E,用含t的式子表示AP和QE,利用三角形的面积即可求解;
(3)根据题意画出矩形即可写出点H的坐标.
(1)根据题意,得
当t=5时,AP=5,AQ=3,
∴B(8,0),A(0,6),
∴OB=8,OA=6,∴AB=10,
∴![]() =
=![]() =
=![]() ,∠PAQ=∠BAO,
,∠PAQ=∠BAO,
∴△APQ∽△ABO;
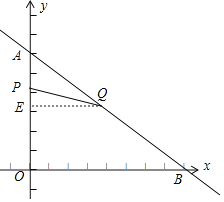
(2)如图:
过点Q作QE⊥OA于点E,
在Rt△AOB和Rt△AQE中,
sin∠BAO=![]() =
=![]() ,sin∠QAE=
,sin∠QAE=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QE=![]() t,
t,
∴S△APQ=![]() APQE=16,
APQE=16,
即![]() ×t×
×t×![]() t=16
t=16
∴t=2![]() .
.
答:那么2![]() 秒时,△APQ的面积为16.
秒时,△APQ的面积为16.
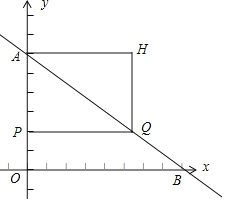
(3)如图:
设点Q的速度为每秒x个单位长度,
当t=4时,AP=4,AQ=4x,
∵以点A,P,H,Q四点为顶点的四边形是矩形,
∴PQ∥OB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PQ=![]() ,
,
∴H(![]() ,6).
,6).
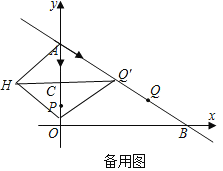
设点Q的速度为每秒x个单位长度,
当t=4时,AP=4,AQ=4x,
∵以点A,P,H,Q四点为顶点的四边形是矩形,
当AP为矩形对角线时,
![]() =
=![]()
解得x=![]()
∴Q′C=![]() =
=![]() .
.
∴H(﹣![]() ,4).
,4).
所以点H的坐标为:(![]() ,6).(﹣
,6).(﹣![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
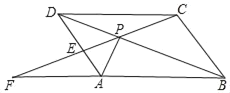
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
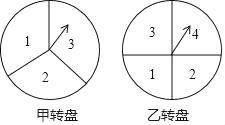
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,将矩形ABCD折叠,使点C与点A重合,点D落在点G处,折痕为EF.
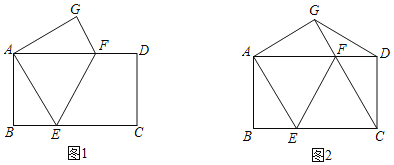
(1)如图1,求证:BE=GF;
(2)如图2,连接CF、DG,若CE=2BE,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形都为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”,通过数形结合,给出了勾股定理的详细证明如图,在“勾股弦方图”中,以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”,若正方形ABCD与正方形EFCH的面积分别为169和49,则所用细塑料棒的长度为______.
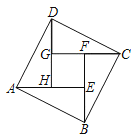
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?
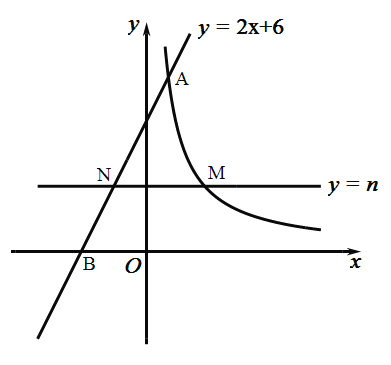
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按照逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按照逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P8的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法正确的有( )
①正八边形的每个内角都是135°;
②反比例函数y=﹣![]() ,当x<0时,y随x的增大而增大;
,当x<0时,y随x的增大而增大;
③长度等于半径的弦所对的圆周角为30°;
④分式方程![]() 的解为
的解为![]() ;
;
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如果α,β都为锐角,且tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
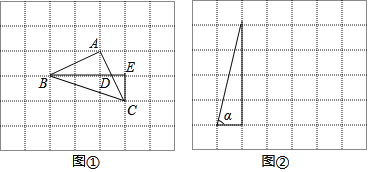
解决:如图①,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,连结AC,易证△ABC是等腰直角三角形,因此可求得α+β=∠ABC= .
拓展:参考以上方法,解决下列问题:如果α,β都为锐角,当tanα=4,tanβ=![]() 时,
时,
(1)在图②的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β;
(2)求出α﹣β= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com