
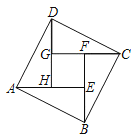
【题目】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”,通过数形结合,给出了勾股定理的详细证明如图,在“勾股弦方图”中,以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”,若正方形ABCD与正方形EFCH的面积分别为169和49,则所用细塑料棒的长度为______.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
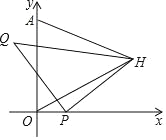
【题目】如图,在平面直角坐标系中,已知Q(﹣1,3),A(0,4),点P为x轴上一动点,以QP为腰作等腰Rt△QPH,当OH+AH最小时,点H的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
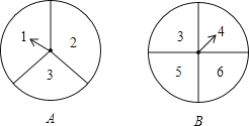
【题目】 如图,有两个可以自由转动的均匀转盘![]() 转盘A被平均分成3等份,分别标上
转盘A被平均分成3等份,分别标上![]() 三个数字;转盘B被平均分成4等份,分别标上
三个数字;转盘B被平均分成4等份,分别标上![]() 四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
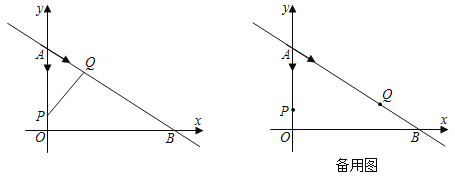
【题目】如图在平面直角坐标系xOy中,直线y=﹣![]() x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
(1)如果点Q的速度为每秒![]() 个单位长度,那么当t=5时,求证:△APQ∽△ABO;
个单位长度,那么当t=5时,求证:△APQ∽△ABO;
(2)如果点Q的速度为每秒2个单位长度,那么多少秒时,△APQ的面积为16?
(3)若点H为平面内任意一点,当t=4时,以点A,P,H,Q四点为顶点的四边形是矩形,请直接写出此时点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
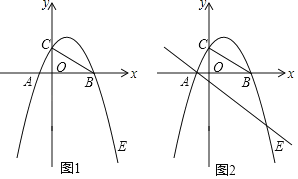
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+m﹣1交x轴于A、B两点,交y轴于点C,若A点坐标为(x1,0),B点坐标为(x2,0)(x1≠x2).
x+m﹣1交x轴于A、B两点,交y轴于点C,若A点坐标为(x1,0),B点坐标为(x2,0)(x1≠x2).
(1)求m的取值范围;
(2)如图1,若x12+x22=17,求抛物线的解析式;
(3)在(2)的条件下,请解答下列两个问题:
①如图1,请连接AC,求证:△ACB为直角三角形.
②如图2,若D(1,n)在抛物线上,过点A的直线y=﹣x﹣1交(2)中的抛物线于点E,那么在x轴上点B的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE相似?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:有这样一个问题:关于x的一元二次方程ax2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:
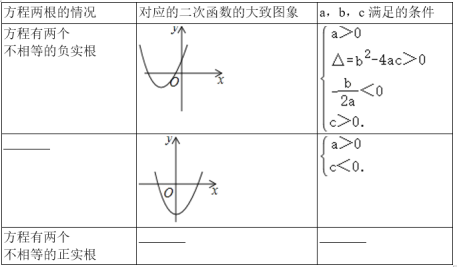
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程mx2﹣(2m+3)x﹣4m=0有一个负实根,一个正实根,且负实根大于﹣1,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果某点的横坐标与纵坐标的和为10,则称此点为“合适点”例如,点(1,9),(﹣2019,2029)…都是“合适点”.
(1)求函数y=2x+1的图象上的“合适点”的坐标;
(2)求二次函数y=x2﹣5x﹣2的图象上的两个“合适点”A,B之间线段的长;
(3)若二次函数y=ax2+4x+c的图象上有且只有一个合适点”,其坐标为(4,6),求二次函数y=ax2+4x+c的表达式;
(4)我们将抛物线y=2(x﹣n)2﹣3在x轴下方的图象记为G1,在x轴及x轴上方图象记为G2,现将G1沿x轴向上翻折得到G3,图象G2和图象G3两部分组成的记为G,当图象G上恰有两个“合适点”时,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com