
【题目】如图,∠CAB=∠ABD=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.连接MB,NA.
(1)求证:四边形MBNA为平行四边形;
(2)当α=____°时,四边形MBNA为矩形;
(3)当α=_____°时,四边形MBNA为菱形;
(4)四边形MBNA可能是正方形吗?_____(回答“可能”或“不可能”)

【答案】(1)证明见解析;(2)80;(3)90;(4)不可能.
【解析】
(1)由“AAS”可证△APM≌△BPN,可得AM=BN,即可得结论;
(2)由矩形的性质和三角形的内角和定理可求解;
(3)由菱形的性质可求解;
(4)由正方形的性质可求解.
(1) 证明:∵P为AB中点,
∴AP=BP
∵∠CAB=∠ABD=50°,
∴AM∥BN
∴∠AMP=∠BNP,且AP=BP,∠CAB=∠ABD=50°,
∴△APM≌△BPN(AAS)
∴AM=BN,且AM∥BN
∴四边形MBNA为平行四边形;
(2)若四边形MBNA为矩形
∴BP=AP=MP=NP
∴∠ABN=∠MNB=50°
∴α=180°﹣50°﹣50°=80°
故答案为:80
(3)若四边形MBNA为菱形
∴AB⊥MN
∴α=90°
故答案为:90
(4)若四边形MBNA为正方形
∴∠ABD=45°≠50°
∴四边形MBNA不可能为正方形
故答案为:不可能


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
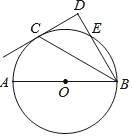
【题目】如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
(1)求证:BC平分∠DBA;
(2)连接AE和AC,若cos∠ABD=![]() ,OA=m,请写出求四边形AEDC面积的思路.
,OA=m,请写出求四边形AEDC面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工地一个工程有大量的沙石需要运输.建设公司车队有载重量为8吨和10吨的卡车共14辆,全部车辆一次能运输128吨沙石.
(1)求建设公司车队载重量为8吨和10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石超过190吨,为了完成任务,准备新增购这两种卡车共7辆,车队最多新购买载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
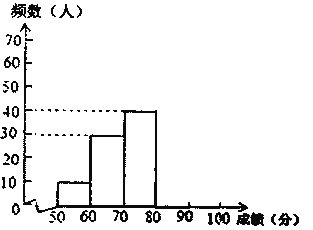
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经
了解得到以下信息(如表):
工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
甲队 | 30 | n | 600 |
乙队 | m | n﹣14 | 1160 |
(1)甲队单独完成这项工程所需天数n= ,乙队每天修路的长度m= (米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,动点M,N分别从A,C同时向B,D匀速移动,且两点的运动速度相同,当动点M到达B点时,M,N同时停止运动,过点N作NP⊥CD,交BD于P点,当△BMP为等腰三角形时,AM=_____.
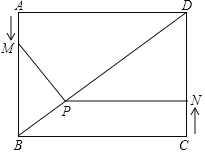
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,以CD为底边在正方形外侧作等腰△CDE,连接BE与对角线AC交于点P、与CD交于点H,连接PD.
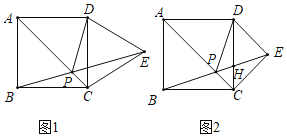
(1)如图1,当∠DEC=60°时,求证:PA=PE;
(2)如图2,当∠DEC=90°时,
①求tan∠EBC的值;②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
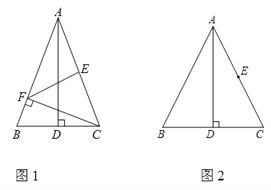
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级在区体育检测前进行最后一次摸底考试,从中随机抽取了50名男生的1000米测试成绩,根据评分标准按A、B、C、D四个等级进行统计,并绘制成下面的扇形图和统计表:
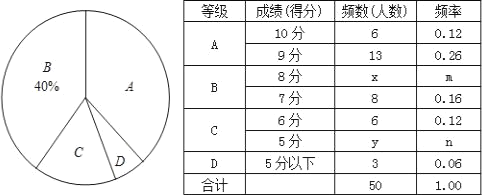
请你根据以上图表提供的信息,解答下列问题:
(1)在统计表中x= ,y= ,m= ,n= ;
(2)在扇形图中,A等级所对应的圆心角是 度;
(3)在50名学生的1000米跑成绩(得分)中,中位数是 ,众数是 ;
(4)如果该校九年级男生共有200名,那么请你估计这200名男生中成绩等级没有达到A或B的共有 人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com