
【题目】某校九年级在区体育检测前进行最后一次摸底考试,从中随机抽取了50名男生的1000米测试成绩,根据评分标准按A、B、C、D四个等级进行统计,并绘制成下面的扇形图和统计表:
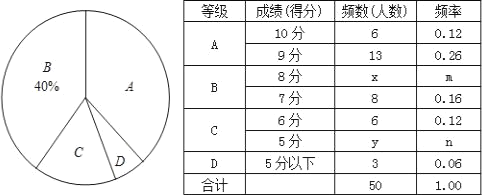
请你根据以上图表提供的信息,解答下列问题:
(1)在统计表中x= ,y= ,m= ,n= ;
(2)在扇形图中,A等级所对应的圆心角是 度;
(3)在50名学生的1000米跑成绩(得分)中,中位数是 ,众数是 ;
(4)如果该校九年级男生共有200名,那么请你估计这200名男生中成绩等级没有达到A或B的共有 人?
【答案】(1)12,2,0.24,0.04;(2)136.8;(3)8分,9分;(4)44.
【解析】
(1)根据B组所占比例求得的比例和总人数求出该组的人数,减去8即得到x的值,然后除以总人数求得该组的总人数;
(2)该组的频率即为该扇形圆心角所占圆周角的比例,所以用圆周角乘以该组的频率即得到该组所表示的扇形的圆心角;
(3)排序后位于中间位置的数分别是8、8,所以中位数是8,9分出现了13次最多,所以众数为9分;
(4)根据没有达到此标准的学生所占的比例求出全校没有达到此标准的学生数.
(1)50×40%=20人,
∴20﹣8=12人,12÷50=0.24,
∴x=12,m=0.24,
∵50﹣6﹣13﹣12﹣8﹣6﹣3=2,
∴2÷50=0.04,
∴y=2,n=0.04;
(2)360°×(0.12+0.26)=136.8°;
(3) 排序后位于中间位置的数分别是8、8,所以中位数是8;9分出现了13次最多,所以众数为9分;
(4)200×(0.12+0.04+0.06)=44.


科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠ABD=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.连接MB,NA.
(1)求证:四边形MBNA为平行四边形;
(2)当α=____°时,四边形MBNA为矩形;
(3)当α=_____°时,四边形MBNA为菱形;
(4)四边形MBNA可能是正方形吗?_____(回答“可能”或“不可能”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
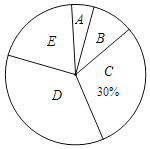
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
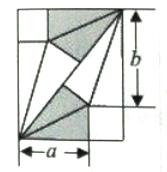
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2-5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
电脑型号 | ① | ② | ③ |
工时(个) |
|
|
|
产值(万元) | 0.4 | 0.3 | 0.2 |
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点O是AB边上一点,以O为圆心OB为半径的⊙O与边AB相交于点E,与AC边相切于D点,连接OC交⊙O于点F.
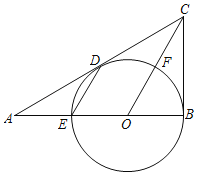
(1)连接DE,求证:OC∥DE;
(2)若⊙O的半径为3.
①连接DF,若四边形OEDF为菱形,弧BD的长为_____(结果保留π)
②若AE=2,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
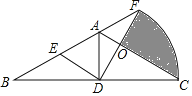
【题目】如图,已知AD是等腰三角形ABC底边BC上的高,AD=1,DC=![]() ,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,当EF与直线AB重合时,设AC与DF相交于点O,那么由线段OC、OF和弧CF围成的阴影部分的面积为_____.
,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,当EF与直线AB重合时,设AC与DF相交于点O,那么由线段OC、OF和弧CF围成的阴影部分的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com