
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点O是AB边上一点,以O为圆心OB为半径的⊙O与边AB相交于点E,与AC边相切于D点,连接OC交⊙O于点F.
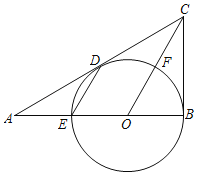
(1)连接DE,求证:OC∥DE;
(2)若⊙O的半径为3.
①连接DF,若四边形OEDF为菱形,弧BD的长为_____(结果保留π)
②若AE=2,则AD的长为_____.
【答案】(1)见解析;(2)①2π;②4.
【解析】
(1)利用HL可证明Rt△OCD≌Rt△OCB,可得∠COD=∠COB,利用三角形外角性质可得∠DOB=∠ODE+∠OED,即可证明∠DOC=∠ODE,即可得OC//DE;(2)①根据菱形的性质可求出∠BOD,利用弧长公式即可得答案;②由DE∥OC,推出![]() =
=![]() =
=![]() ,设AD=2k,CD=3k,由Rt△OCD≌Rt△OCB,可得BC=CD=3k,在Rt△ABC中,利用勾股定理构建方程即可解决问题.
,设AD=2k,CD=3k,由Rt△OCD≌Rt△OCB,可得BC=CD=3k,在Rt△ABC中,利用勾股定理构建方程即可解决问题.
(1)证明:连接OD.
∵AC是切线,
∴OD⊥AC,∠ODC=∠OBC=90°,
∵OC=OC,OD=OB,
∴Rt△OCD≌Rt△OCB(HL),
∴∠COD=∠COB,
∵OD=OE,
∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,
∴∠DOC=∠ODE,
∴DE∥OC.

(2)①∵四边形DEOF是菱形,
∴DF=OD=OF,
∴△ODF是等边三角形,
∴∠DOF=60°,
∴∠BOD=2∠DOC=120°,
∴![]() 的长=
的长=![]() =2π.
=2π.
故答案为2π.
②∵DE∥OC,
∴![]() =
=![]() =
=![]() ,
,
设AD=2k,CD=3k,
∵Rt△OCD≌Rt△OCB,
∴BC=CD=3k,
在Rt△ABC中,则有25k2=9k2+82,
∴k=2或﹣2(舍弃),
∴AD=4.
故答案为4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,以CD为底边在正方形外侧作等腰△CDE,连接BE与对角线AC交于点P、与CD交于点H,连接PD.
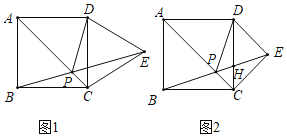
(1)如图1,当∠DEC=60°时,求证:PA=PE;
(2)如图2,当∠DEC=90°时,
①求tan∠EBC的值;②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级在区体育检测前进行最后一次摸底考试,从中随机抽取了50名男生的1000米测试成绩,根据评分标准按A、B、C、D四个等级进行统计,并绘制成下面的扇形图和统计表:
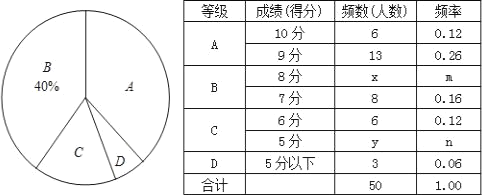
请你根据以上图表提供的信息,解答下列问题:
(1)在统计表中x= ,y= ,m= ,n= ;
(2)在扇形图中,A等级所对应的圆心角是 度;
(3)在50名学生的1000米跑成绩(得分)中,中位数是 ,众数是 ;
(4)如果该校九年级男生共有200名,那么请你估计这200名男生中成绩等级没有达到A或B的共有 人?
查看答案和解析>>
科目:初中数学 来源: 题型:
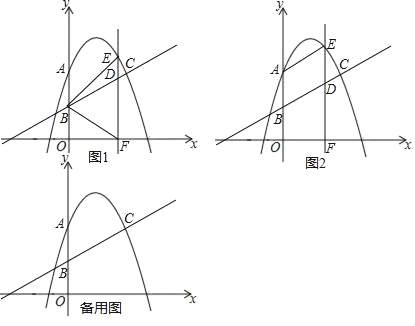
【题目】如图,抛物线y=﹣x2+bx+c经过A(0,3),C(2,n)两点,直线l:y=![]() x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
(1)求抛物线的解析式.
(2)如图1,当点E在直线BC上方的抛物线上运动时,连接BE,BF,是否存在点E使直线BC将△BEF的面积分为2:3两部分?若存在,求出点E的坐标,若不存在说明理由;
(3)如图2,若点E在y轴右侧的抛物线上运动,连接AE,当∠AED=∠ABC时,直接写出此时点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(0,3),C(2,n)两点,直线l:y=![]() x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
(1)求抛物线的解析式.
(2)如图1,当点E在直线BC上方的抛物线上运动时,连接BE,BF,是否存在点E使直线BC将△BEF的面积分为2:3两部分?若存在,求出点E的坐标,若不存在说明理由;
(3)如图2,若点E在y轴右侧的抛物线上运动,连接AE,当∠AED=∠ABC时,直接写出此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
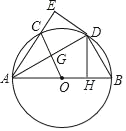
【题目】如图,Rt△ADB中,∠ADB=90°,∠DAB=30°,⊙O为△ADB的外接圆,DH⊥AB于点H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.
(1)求证:DE是⊙O的切线;
(2)若AB=10,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
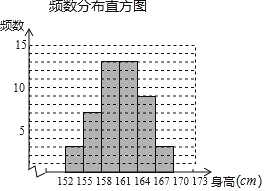
【题目】下表统计的是甲、乙两班男生的身高情况,根据统计表绘制了如下不完整的统计图.
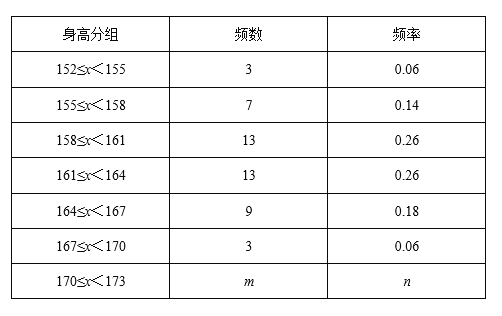
根据以上统计表完成下列问题:
(1)统计表中的m= ,n= ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在 范围内;
(3)在身高不低于167cm的男生中,甲班有2人.现从这些身高不低于167cm的男生中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
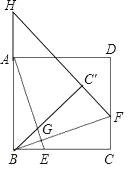
【题目】如图,在正方形ABCD中,点E、F分别在边BC和CD上,且BE=CF,连接AE、BF,其相交于点G,将△BCF沿BF翻折得到△BC′F,延长FC′交BA延长线于点H.
(1)①求证:AE=BF;
②猜想AE与BF的位置关系,并证明你的结论;
(2)若AB=3,EC=2BE,求BH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com