
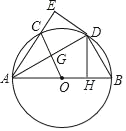
【题目】如图,Rt△ADB中,∠ADB=90°,∠DAB=30°,⊙O为△ADB的外接圆,DH⊥AB于点H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.
(1)求证:DE是⊙O的切线;
(2)若AB=10,求线段OG的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接半径,由同圆的半径相等得:OA=OD,利用等边对等角可知:∠OAD=∠ODA,利用翻折的性质可知:∠OAD=∠EAD,∠E=∠AHD=90°,证OD∥AE,得∠ODE=90°,所以DE与⊙O相切;
(2)先证明△OAC是等边三角形,再证明OG∥BD,根据中位线定理可知:BD=2OG=5,于是得到结论.
解:(1)连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
由翻折得:∠OAD=∠EAD,∠E=∠AHD=90°,
∴∠ODA=∠EAD,
∴OD∥AE,
∴∠E+∠ODE=180°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)∵将△AHD沿AD翻折得到△AED,
∴∠OAD=∠EAD=30°,
∴∠OAC=60°,
∵OA=OD,
∴△OAC是等边三角形,
∴∠AOG=60°,
∵∠OAD=30°,
∴∠AGO=90°,
∴OG=![]() AO=
AO=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
(1)为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理的是 ;
A.对某小区的住户进行问卷调查
B.对某班的全体同学进行问卷调查
C.在市里的不同地铁站,对进出地铁的人进行问卷调查
(2)调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.

① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是 元;
A.20—60 B.60—120 C.120—180
②为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到 元的人可以享受折扣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2-5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点O是AB边上一点,以O为圆心OB为半径的⊙O与边AB相交于点E,与AC边相切于D点,连接OC交⊙O于点F.
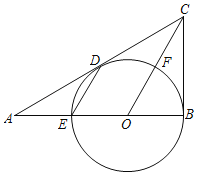
(1)连接DE,求证:OC∥DE;
(2)若⊙O的半径为3.
①连接DF,若四边形OEDF为菱形,弧BD的长为_____(结果保留π)
②若AE=2,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx-1经过点A(-2,1)和点B(-1,-1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表示线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
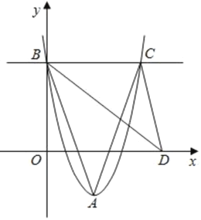
【题目】如图,在平面直角坐标系中,点A是抛物线y=ax2+bx+c的顶点,点B(0,2)是抛物线与y轴的交点,直线BC平行于x轴,交抛物线于点C,D为x轴上任意一点,若S△ABC=3,S△BCD=2,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点M从点A出发,沿A→B→C方向运动,当点M到达点C时停止运动,过点M作MN⊥AM交CD于点N,设点M的运动路程为x,CN=y,图2表示的是y与x的函数关系的大致图象,则矩形ABCD的面积是( )
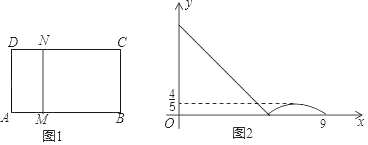
A.20B.18C.10D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com