
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������C1��y=ax2+bx-1������A��-2��1���͵�B��-1��-1����������C2��y=2x2+x+1����ֱ��x=t��������C1���ڵ�N����������C2���ڵ�M��
��1����������C1�ı���ʽ��
��2��ֱ���ú�t�Ĵ���ʽ��ʾ�߶�MN�ij���
��3������AMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����t��ֵ��
��4���ڣ�3���������£���������C1��y�ύ�ڵ�P����M��y���Ҳ��������C2�ϣ�����AM��y���ڵ�K������KN����ƽ������һ��Q������KQ��QN����KQ=1�ҡ�KNQ=��BNPʱ����ֱ��д����Q�����꣮

���𰸡���1��y��x2��x��1����2��t2+2����3��1��0����4��Q������Ϊ����0��2������-1��3����![]() .
.
��������
��1��Ӧ�ô���ϵ������
��2����x=t���뺯����ϵʽ�����
��3������ͼ�ηֱ����ۡ�ANM=90������AMN=90��ʱ�������
��4���������⻭����������ͼ�Σ������ҵ�ANΪ��KNP�Գ��ᣬ�ɶԳ����ҵ���һ����������Q����ͨ���ӳ���Բ�ĶԳ����ҵ�ʣ�������㣮���ù��ɶ������м��㣮
��1������������C1��y��ax2��bx��1������A����2��1���͵�B����1����1����
��![]() ��
��
���![]() ��
��
����������C1�Ľ���ʽΪy��x2��x��1��
��2���߶�ֱ��x=t��������C1���ڵ�N����������C2���ڵ�M
���N��������Ϊt2+t-1����M��������Ϊ2t2+t+1
��MN=��2t2+t+1��-��t2+t-1��=t2+2
��3�������������
�ٵ���ANM=90����AN=MNʱ������֪N��t��t2+t-1����A��-2��1��
��AN=t-��-2��=t+2
��MN=t2+2
��t2+2=t+2
��t1=0����ȥ����t2=1
��t=1
�ڵ���AMN=90����AM=MNʱ������֪M��t��2t2+t+1����A��-2��1��
��AM=t-��-2��=t+2��
��MN=t2+2
��t2+2=t+2
��t1=0��t2=1����ȥ��
��t=0
��t��ֵΪ1��0
��4���ɣ�3����֪t=1ʱMλ��y���Ҳ࣬�������⻭��ʾ��ͼ��ͼ��

��K��0��3����B��O��N���㹲��
��A��-2��1��N��1��1��P��0��-1��
���K��P����ֱ��AN�Գ�
��뾶Ϊ1�ġ�K��y���·�����ΪQ2����������Ϊ��0��2��
��Q2���O����ֱ��AN�Գ�
��Q2������������KNQ=��BNP��
��NQ2�ӳ������K����Q1��Q1��Q2����KN�ĶԳƵ�Q3��Q4Ҳ�����KNQ=��BNP��
��ͼ����Q1��-1��3��
���Q3����Ϊ��m��n�����ɶԳ��Կ�֪Q3N=NQ1=BN=2![]()
�ɡߡ�K�뾶Ϊ1
��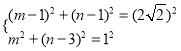
��� ����
����
ͬ�������Q4����Ϊ��m��n�����ɶԳ��Կ�֪Q4N=NQ2=NO=![]()
��
��� ��
��
������������Q����������0��2������-1��3����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O������B������BE��AC����P���Ż�AC��һ����(����A��C�غ�)������PA��PB��PC��PB��AC��D��
(1)��֤��PBƽ�֡�APC��
(2)��PD��3��PB��4ʱ����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����x2+bx+c����A(0��3)��C(2��n)���㣬ֱ��l��y��![]() x+2��C�㣬����y�ύ�ڵ�B������������һ����E������E��ֱ��EF��x���ڵ�F����ֱ��BC�ڵ�D
x+2��C�㣬����y�ύ�ڵ�B������������һ����E������E��ֱ��EF��x���ڵ�F����ֱ��BC�ڵ�D
(1)�������ߵĽ���ʽ��
(2)��ͼ1������E��ֱ��BC�Ϸ������������˶�ʱ������BE��BF���Ƿ���ڵ�Eʹֱ��BC����BEF�������Ϊ2��3�����֣������ڣ������E�����꣬��������˵�����ɣ�
(3)��ͼ2������E��y���Ҳ�����������˶�������AE������AED����ABCʱ��ֱ��д����ʱ��E�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
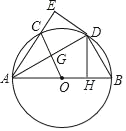
����Ŀ����ͼ��Rt��ADB�У���ADB��90������DAB��30������OΪ��ADB�����Բ��DH��AB�ڵ�H���ֽ���AHD��AD���۵õ���AED��AE����O�ڵ�C������OC��AD�ڵ�G��
��1����֤��DE�ǡ�O�����ߣ�
��2����AB��10�����߶�OG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ӡ�����ӽ���������������ܵ����㷺��ע������ijУ�͡��л��Ļ��Ҵ��С����ط�Ϸ����У����ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ���ṩ����Ϣ����������⣺

ͼ��A��ʾ����ϲ������B��ʾ��ϲ������C��ʾ��һ�㡱��D��ʾ����ϲ������
��1�����������������_____�ˣ�����ͳ��ͼ��C��������Ӧ������Բ�ĽǵĶ���Ϊ_____��
��2���ٲ�ȫ����ͳ��ͼ��������У����ѧ��1800�ˣ���������������������Ƹ�Уѧ����A���ж����ˣ�
��3���ڳ�ȡ��A��5���У��պ���3��Ů��2�����������������ȡ����ͬѧ��������ɫ��������ͼ���б���������鵽������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±�ͳ�Ƶ��Ǽס��������������������������ͳ�Ʊ����������²�������ͳ��ͼ��
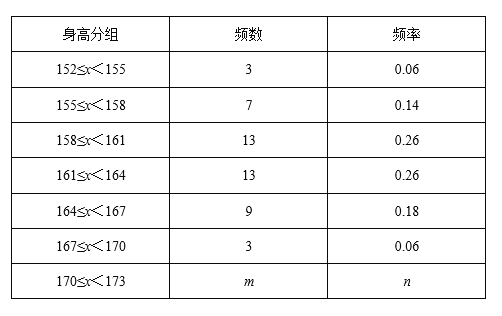
��������ͳ�Ʊ�����������⣺
��1��ͳ�Ʊ��е�m���� ����n���� ��������Ƶ���ֲ�ֱ��ͼ����������
��2������β����������������ߵ���λ������ ����Χ�ڣ�
��3�������߲�����167cm�������У��װ���2�ˣ��ִ���Щ���߲�����167cm�������������ѡ2�˲��䵽ѧУ���커�����У������б�����״ͼ�ķ�����������˶�������ͬ�༶�ĸ��ʣ�
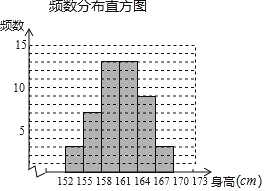
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ܼ��ţ�������������ij��ƻ�����A��B�����ͺŵ������ع�20�����Խ������ũ����ȼ�����⣮���г����飺����A��B�����ͺŵ������ظ�1�����������5��Ԫ������A�ͺŵ�������3����B���ͺŵ�������4�����������18��Ԫ��
��1������A��B�����ͺŵ���������۷ֱ��Ƕ��٣�
��2���轨��A��������x�����ܷ���Ϊy��Ԫ����y��x֮��ĺ�����ϵʽ����ҪʹͶ���ܷ��ò�����52��Ԫ������Ҫ����A�������ض��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
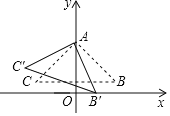
����Ŀ����ͼ����Rt��ABC�У���CAB��90�㣬AB��AC����A��y���ϣ�BC��x�ᣬ��B![]() ������ABC�Ƶ�A˳ʱ����ת�ġ�AB��C�䣬����B������x�����������ʱ����C�������Ϊ��������
������ABC�Ƶ�A˳ʱ����ת�ġ�AB��C�䣬����B������x�����������ʱ����C�������Ϊ��������
A.����![]() ��
��![]() ��1��B.����
��1��B.����![]() ��
��![]() ��1��
��1��
C.����![]() ��
��![]() +1��D.����
+1��D.����![]() ��
��![]() ��1��
��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com