
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:

图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____人,扇形统计图中C部分所对应的扇形圆心角的度数为_____;
(2)①补全条形统计图;②若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有多少人;
(3)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
【答案】(1)50,216°;(2)①见解析;②180人;(3)见解析,![]() .
.
【解析】
(1)由A类别人数及其所占百分比可得总人数,用360°乘以C部分人数所占比例可得;
(2)①总人数减去其他类别人数求得B的人数,据此即可补全条形图;
②用总人数乘以样本中A类别人数所占百分比可得;
(3)用树状图或列表法即可求出抽到性别相同的两个学生的概率.
(1)被调查的总人数为5÷10%=50人,扇形统计图中C部分所对应的扇形圆心角的度数为360°×![]() =216°,
=216°,
故答案为:50、216°;
(2)①补全条形图如下:

②估计该校学生中A类有1800×10%=180人;
(3)列表如下:
女1 | 女2 | 女3 | 男1 | 男2 | |
女1 | 女2女1 | 女3女1 | 男1女1 | 男2女1 | |
女2 | 女1女2 | 女3女2 | 男1女2 | 男2女2 | |
女3 | 女1女3 | 女2女3 | 男1女3 | 男2女3 | |
男1 | 女1男1 | 女2男1 | 女3男1 | 男2男1 | |
男2 | 女1男2 | 女2男2 | 女3男2 | 男1男2 |
由上表可知:所有等可能的结果为20种,其中被抽到的两个学生性别相同的结果数为8,∴被抽到的两个学生性别相同的概率为![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴的交点为A,B.按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交AB,x轴于点C,D;②分别以点C,D为圆心,大于
与x轴、y轴的交点为A,B.按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交AB,x轴于点C,D;②分别以点C,D为圆心,大于![]() 的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交y轴于点E.则点E的坐标为( )
的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交y轴于点E.则点E的坐标为( )

A.(0,![]() )B.(0,
)B.(0,![]() )C.(0,
)C.(0,![]() )D.(0,
)D.(0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
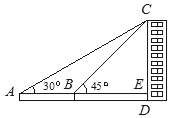
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了40m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(结果精确到1m)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx-1经过点A(-2,1)和点B(-1,-1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表示线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC;
(2)若DM:DB=2:5,求证:AN=4BN;
(3)如图②,连接NC交BD于点G.若BG:MG=3:5,求NGCG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com