
ĄūĖâÄŋĄŋžŨĄĒŌŌÁ―ģĩ·ÖąðīÓÏāūā420kmĩÄAĄĒBÁ―ĩØÏāÏōķøÐÐĢŽŌŌģĩąČžŨģĩÏČģö·Ē1ÐĄĘąĢŽÁ―ģĩ·ÖąðŌÔļũŨÔĩÄËŲķČÔČËŲÐÐĘŧĢŽÍūūCĩØĢĻAĄĒBĄĒCČýĩØÔÚÍŽŌŧĖõÖąÏßÉÏĢĐĢŪžŨģĩĩ―īïCĩØšóŌōÓÐĘÂÁĒžī°īÔ·ÔËŲ·ĩŧØAĩØĢŽŌŌģĩīÓBĩØÖąīïAĩØĢŽžŨĄĒŌŌÁ―ģĩūāļũŨÔģö·ĒĩØĩÄ·ģĖyĢĻĮ§ÃŨĢĐÓëžŨģĩÐÐĘŧËųÓÃĩÄĘąžäxĢĻÐĄĘąĢĐĩÄđØÏĩČįÍžËųĘūĢŽ―ášÏÍžÏóÐÅÏĒŧØīðÏÂÁÐÎĘĖâĢš
ĢĻ1ĢĐžŨģĩĩÄËŲķČĘĮĄĄ ĄĄĮ§ÃŨ/ĘąĢŽŌŌģĩĩÄËŲķČĘĮĄĄ ĄĄĮ§ÃŨ/ĘąĢŧ
ĢĻ2ĢĐĮóžŨģĩūāËüģö·ĒĩØĩÄ·ģĖyĢĻĮ§ÃŨĢĐÓëËüÐÐĘŧËųÓÃĩÄĘąžäxĢĻÐĄĘąĢĐÖŪžäĩÄšŊĘýđØÏĩĘ―Ģŧ
ĢĻ3ĢĐžŨģĩģö·ĒķāģĪĘąžäšóÁ―ģĩÏāūā90Į§ÃŨĢŋĮëÄãÖą―ÓÐīģöīð°ļĢŪ

Ąūīð°ļĄŋĢĻ1ĢĐ105ĢŽ60ĢŧĢĻ2ĢĐyĢ―![]() ĢŧĢĻ3ĢĐ
ĢŧĢĻ3ĢĐ![]() ĘąĢŽ
ĘąĢŽ![]() Ęąŧō
Ęąŧō![]() ĘąĢŪ
ĘąĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝĖâŌâšÍšŊĘýÍžÏóÖÐĩÄĘýūÝŋÉŌÔĩÃĩ―žŨŌŌÁ―ģĩĩÄËŲķČĢŧ
ĢĻ2ĢĐļųūÝĖâŌâšÍšŊĘýÍžÏóÖÐĩÄĘýūÝŋÉŌÔĮóĩÞŨģĩūāËüģö·ĒĩØĩÄ·ģĖyĢĻĮ§ÃŨĢĐÓëËüÐÐĘŧËųÓÃĩÄĘąžäxĢĻÐĄĘąĢĐÖŪžäĩÄšŊĘýđØÏĩĘ―Ģŧ
ĢĻ3ĢĐļųūÝĖâŌâŋÉÖŠžŨŌŌÁ―ģĩÏāūā90Į§ÃŨ·ÖÁ―ÖÖĮéŋöĢŽīÓķøŋÉŌÔ―âīðąūĖâĢŪ
ĢĻ1ĢĐÓÉÍžŋÉĩÃĢŽ
žŨģĩĩÄËŲķČΊĢšĢĻ210ĄÁ2ĢĐĄÂ4Ģ―420ĄÂ4Ģ―105Į§ÃŨ/ĘąĢŽ
ŌŌģĩĩÄËŲķČΊĢš60Į§ÃŨ/ĘąĢŽ
đĘīð°ļΊĢš105ĢŽ60Ģŧ
ĢĻ2ĢĐÓÉÍžŋÉÖŠĢŽĩãMĩÄŨøąęΊĢĻ2ĢŽ210ĢĐĢŽ
ĩą0ĄÜxĄÜ2ĘąĢŽÉčyĢ―k1xĢŽ
ĄßMĢĻ2ĢŽ210ĢĐÔÚļÚŊĘýÍžÏóÉÏĢŽ
2k1Ģ―210ĢŽ
―âĩÃĢŽk1Ģ―105ĢŽ
ĄāyĢ―105xĢĻ0ĄÜxĄÜ2ĢĐĢŧ
ĩą2ĢžxĄÜ4ĘąĢŽÉčyĢ―k2x+bĢŽ
ĄßMĢĻ2ĢŽ210ĢĐšÍĩãNĢĻ4ĢŽ0ĢĐÔÚļÚŊĘýÍžÏóÉÏĢŽ
Ąā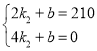 ĢŽĩÃ
ĢŽĩÃ![]() ĢŽ
ĢŽ
ĄāyĢ―Đ105x+420ĢĻ2ĢžxĄÜ4ĢĐĢŽ
ŨÛÉÏËųĘöĢšžŨģĩūāËüģö·ĒĩØĩÄ·ģĖyÓëËüģö·ĒĩÄĘąžäxĩÄšŊĘýđØÏĩĘ―ÎŠĢšyĢ―![]() Ģŧ
Ģŧ
ĢĻ3ĢĐÉčžŨģĩģö·ĒaÐĄĘąĘąÁ―ģĩÏāūā90Į§ÃŨĢŽ
ĩąžŨīÓAĩØĩ―CĩØĘąĢŽ
105a+60ĢĻa+1ĢĐ+90Ģ―420ĢŽ
―âĩÃĢŽaĢ―![]() ĢŽ
ĢŽ
ĩąžŨīÓCĩØ·ĩŧØAĩØĘąĢŽ
ĢĻ210Đ60ĄÁ3ĢĐ+ĢĻ105Đ60ĢĐĄÁĢĻaĐ2ĢĐĢ―90ĢŽ
―âĩÃĢŽaĢ―![]() ĢŽ
ĢŽ
ĩąžŨĩ―īïAĩØšóĢŽ
420Đ60ĢĻa+1ĢĐĢ―90ĢŽ
―âĩÃĢŽaĢ―![]() ĢŽ
ĢŽ
īðĢšžŨģĩģö·Ē![]() ĘąĢŽ
ĘąĢŽ![]() Ęąŧō
Ęąŧō![]() ĘąĢŽÁ―ģĩÏāūā90Į§ÃŨĢŪ
ĘąĢŽÁ―ģĩÏāūā90Į§ÃŨĢŪ


 ÃûÐĢŋÎĖÃÏĩÁÐīð°ļ
ÃûÐĢŋÎĖÃÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÖą―ĮĄũABCÖÐĢŽĄÏBAC=90ĄãĢŽDÔÚBCÉÏĢŽÁŽ―ÓADĢŽŨũBFĄÍAD·Öąð―ŧADÓÚEĢŽACÓÚFĢŪ
ĢĻ1ĢĐČįÍž1ĢŽČôBD=BAĢŽĮóÖĪĢšĄũABEĄÕĄũDBEĢŧ
ĢĻ2ĢĐČįÍž2ĢŽČôBD=4DCĢŽČĄABĩÄÖÐĩãGĢŽÁŽ―ÓCG―ŧADÓÚMĢŽĮóÖĪĢšĒŲGM=2MCĢŧĒÚAG2=AFACĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚĻS![]() ÖÐĢŽ
ÖÐĢŽ![]() ,ĩã
,ĩã![]() ·ÖąðÔÚ
·ÖąðÔÚ![]() ąßÉÏĢŽĮŌ
ąßÉÏĢŽĮŌ![]() ,
, ![]() .
.
ĒÅ.ĮóÖĪĢšĻS![]() ĘĮĩČŅüČý―ĮÐÎĢŧ
ĘĮĩČŅüČý―ĮÐÎĢŧ
ĒÆ.ĩą![]() ĘąĢŽĮó
ĘąĢŽĮó![]() ĩÄķČĘý.
ĩÄķČĘý.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
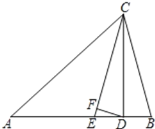
ĄūĖâÄŋĄŋČįÍž,ÔÚĄũABCÖÐ,ĄÏA=![]() ,ĄÏB=
,ĄÏB=![]() ĢŽCDĘĮABąßÉÏĩÄļßĢŧCEĘĮĄÏACBĩÄÆ―·ÖÏßĢŽDFĄÍCEÓÚFĢŽĮóĄÏBCEšÍĄÏCDFĩÄķČĘý.
ĢŽCDĘĮABąßÉÏĩÄļßĢŧCEĘĮĄÏACBĩÄÆ―·ÖÏßĢŽDFĄÍCEÓÚFĢŽĮóĄÏBCEšÍĄÏCDFĩÄķČĘý.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠŌŧīΚŊĘýy=kx+bĩÄÍžÏóūđýĩãĢĻĐ2ĢŽ5ĢĐĢŽēĒĮŌÓëyÖá―ŧÓÚĩãPĢŽÖąÏßy=![]() x+3ÓëyÖá―ŧÓÚĩãQĢŽĩãQĮĄÓëĩãPđØÓÚxÖáķÔģÆĢŽĮóÕâļöŌŧīΚŊĘýĩÄ―âÎöĘ―ĢŪ
x+3ÓëyÖá―ŧÓÚĩãQĢŽĩãQĮĄÓëĩãPđØÓÚxÖáķÔģÆĢŽĮóÕâļöŌŧīΚŊĘýĩÄ―âÎöĘ―ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCÖÐĢŽĄÏABCĄĒĄÏACBĩÄ―ĮÆ―·ÖÏß―ŧÓÚĩãOĢŽđýOĩãŨũMNĄÎBC·Öąð―ŧABĄĒACÓÚMĄĒNÁ―ĩãĢŪABĢ―7ĢŽACĢ―8ĢŽCBĢ―9ĢŽÔōĄũAMNĩÄÖÜģĪĘĮĢĻ ĢĐ

A.14B.16C.17D.15
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚĩČąßČý―ĮÐÎĄũABCÖÐĢŽAEĢ―CDĢŽADĄĒBE―ŧÓÚPĩãĢŽBQĄÍADÓÚQĢŽĮóÖĪĢš
(1) BPĢ―2PQ
(2) ÁŽPCĢŽČôBPĄÍPCĢŽĮó![]() ĩÄÖĩ
ĩÄÖĩ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĩãN(0ĢŽ6)ĢŽĩãMÔÚxÖáļš°ëÖáÉÏĢŽONĢ―3OM.AΊÏßķÎMNÉÏŌŧĩãĢŽABĄÍxÖáĢŽīđŨãΊĩãBĢŽACĄÍyÖáĢŽīđŨãΊĩãC.
(1)ÐīģöĩãMĩÄŨøąęĢŧ
(2)ĮóÖąÏßMNĩÄąíīïĘ―Ģŧ
(3)ČôĩãAĩÄšáŨøąęΊĢ1ĢŽĮóūØÐÎABOCĩÄÃæŧýĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽBĄĒCĄĒEČýĩãÔÚŌŧĖõÖąÏßÉÏĢŽĻSABCšÍĻSDCEķžÎŠĩČąßČý―ĮÐÎĢŽÁŽ―ÓAEĄĒDBĄĒ
ĢĻ1ĢĐĘÔËĩģö AE=BDĩÄĀíÓÉĄĒ

ĢĻ2ĢĐČįđû°ŅĻSDCEČÆCĩãËģĘąÕëÐýŨŠŌŧļö―ĮķČĢŽĘđBĄĒCĄĒEēŧÔÚŌŧĖõÖąÏßÉÏ,ĢĻ1)ÖÐĩÄ―áÂÛŧđģÉÁĒÂðĢŋĢĻÖŧŧØīðĢŽēŧËĩĀíÓÉĢĐ

ĢĻ3ĢĐÔÚĢĻ2ĢĐÖÐČôAEĄĒBDÏā―ŧÓÚP, ĮóĄÏAPBĩÄķČĘýĄĒ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com