Question

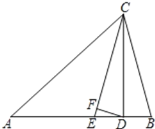
【题目】如图,在△ABC中,∠A=,∠B=，CD是AB边上的高；CE是∠ACB的平分线，DF⊥CE于F，求∠BCE和∠CDF的度数.

Answer 1

【答案】∠BCE=34°，∠CDF=74°．

【解析】

根据三角形内角和定理求出∠ACB，根据角平分线定义求出∠BCE即可，根据直角三角形两锐角互余求出∠BCD，进而求出∠FCD，再根据直角三角形两锐角互余求出∠CDF即可．

∵∠A+∠B+∠ACB=180°，∠A=40°，∠B=72°，∴∠ACB=68°．

∵CE平分∠ACB，∴∠BCE∠ACB68°=34°．

∵CD⊥AB，∴∠CDB=90°．

∵∠B=72°，∴∠BCD=90°﹣72°=18°，∴∠FCD=∠BCE﹣∠BCD=16°．

∵DF⊥CE，∴∠CFD=90°，∴∠CDF=90°﹣∠FCD=74°，即∠BCE=34°，∠CDF=74°．