练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

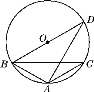
    【题目】如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD为⊙O的直径，AD＝6，则BC＝________．

    【答案】6

    【解析】

    由已知可证∠BDA=30°；根据BD为⊙O的直径，可证∠BAD=90°，得∠DBC=30°，即∠DBA=60°，所以BC=AD=6．

    解：连接CD．

    ∵△ABC内接于⊙O，∠BAC=120°，AB=AC，

    ∴∠CBA=∠BCA=30°．

    ∴∠BDA=∠ACB=30°．

    ∵BD为⊙O的直径，

    ∴∠BAD=90°，∠BDA=30°，

    ∴∠DBC=90°-30°-30°=30°，

    ∴∠DBA=60°，∠BDC=60°，

    ∴BC=AD=6．

    本题重点考查了同弧所对的圆周角相等、直径所对的圆周角为直角及解直角三角形的知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，然后解决问题：和、差、倍、分等问题中有着广泛的应用，

    截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．

    （1）如图1，在△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围．

    解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是 ；

    （2）问题解决：

    如图2，在四边形ABCD中，AB=AD，∠ABC+∠ADC=180°，E、F分别是边BC，边CD上的两点，且∠EAF=∠BAD，求证：BE+DF=EF．

    （3）问题拓展：

    如图3，在△ABC中，∠ACB=90°，∠CAB=60°，点D是△ABC外角平分线上一点，DE⊥AC交CA延长线于点E，F是AC上一点，且DF=DB．求证：AC-AE=AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,∠A=,∠B=，CD是AB边上的高；CE是∠ACB的平分线，DF⊥CE于F，求∠BCE和∠CDF的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ABC、∠ACB的角平分线交于点O，过O点作MN∥BC分别交AB、AC于M、N两点．AB＝7，AC＝8，CB＝9，则△AMN的周长是（ ）

    A.14B.16C.17D.15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形△ABC中，AE＝CD，AD、BE交于P点，BQ⊥AD于Q，求证：

    (1) BP＝2PQ

    (2) 连PC，若BP⊥PC，求的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，AC，PB的延长线相交于点D.

    (1)若∠1＝20°，求∠APB的度数．

    (2)当∠1为多少度时，OP＝OD？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点N(0，6)，点M在x轴负半轴上，ON＝3OM.A为线段MN上一点，AB⊥x轴，垂足为点B，AC⊥y轴，垂足为点C.

    (1)写出点M的坐标；

    (2)求直线MN的表达式；

    (3)若点A的横坐标为－1，求矩形ABOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我省某地区为了了解2016年初中毕业生毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向：A．读普通高中；B．读职业高中；C．直接进入社会就业；D．其他（如出国等）进行数据统计，并绘制了两幅不完整的统计图（如图1，如图2）

    （1）填空：该地区共调查了 名九年级学生；

    （2）将两幅统计图中不完整的部分补充完整；

    （3）若该地区2016年初中毕业生共有3500人，请估计该地区今年初中毕业生中读普通高中的学生人数；

    （4）老师想从甲，乙，丙，丁4位同学中随机选择两位同学了解他们毕业后的去向情况，请用画树状图或列表的方法求选中甲同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，点分别在射线上移动，的平分线与的外角平分线交于点.

    （1）当时， .

    （2）请你猜想：随着两点的移动，的度数大小是否变化？请说明理由.

    查看答案和解析>>

    同步练习册答案