
【题目】如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC;
(2)若DM:DB=2:5,求证:AN=4BN;
(3)如图②,连接NC交BD于点G.若BG:MG=3:5,求NGCG的值.

【答案】(1)见解析;(2)见解析;(3)CGNG=![]() .
.
【解析】
(1)作ME∥AB、MF∥BC,证四边形BEMF是正方形得ME=MF,再证∠CME=∠FMN,从而得△MFN≌△MEC,据此可得证;
(2)由FM∥AD,EM∥CD知![]() =
=![]() =
=![]() =
=![]() ,据此得AF=2.4,CE=2.4,由△MFN≌△MEC知FN=EC=2.4,AN=4.8,BN=6-4.8=1.2,从而得出答案;
,据此得AF=2.4,CE=2.4,由△MFN≌△MEC知FN=EC=2.4,AN=4.8,BN=6-4.8=1.2,从而得出答案;
(3)把△DMC绕点C逆时针旋转90°得到△BHC,连接GH,先证△MCG≌△HCG得MG=HG,由BG:MG=3:5可设BG=3a,则MG=GH=5a,继而知BH=4a,MD=4a,由DM+MG+BG=12a=6![]() 得a=
得a=![]() ,知BG=
,知BG=![]() ,MG=
,MG=![]() ,证△MGC∽△NGB得
,证△MGC∽△NGB得![]() ,从而得出答案.
,从而得出答案.
解:(1)如图①,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,
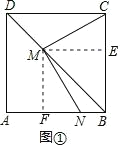
则四边形BEMF是平行四边形,
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,
∴ME=BE,
∴平行四边形BEMF是正方形,
∴ME=MF,
∵CM⊥MN,
∴∠CMN=90°,
∵∠FME=90°,
∴∠CME=∠FMN,
∴△MFN≌△MEC(ASA),
∴MN=MC;
(2)由(1)得FM∥AD,EM∥CD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AF=2.4,CE=2.4,
∵△MFN≌△MEC,
∴FN=EC=2.4,
∴AN=4.8,BN=6﹣4.8=1.2,
∴AN=4BN;
(3)如图②,把△DMC绕点C逆时针旋转90°得到△BHC,连接GH,
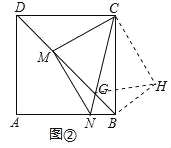
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH=45°,∠DCM=∠BCH,
∴∠MBH=90°,∠MCH=90°,
∵MC=MN,MC⊥MN,
∴△MNC是等腰直角三角形,
∴∠MNC=45°,
∴∠NCH=45°,
∴△MCG≌△HCG(SAS),
∴MG=HG,
∵BG:MG=3:5,
设BG=3a,则MG=GH=5a,
在Rt△BGH中,BH=4a,则MD=4a,
∵正方形ABCD的边长为6,
∴BD=6![]() ,
,
∴DM+MG+BG=12a=6![]() ,
,
∴a=![]() ,
,
∴BG=![]() ,MG=
,MG=![]() ,
,
∵∠MGC=∠NGB,∠MNG=∠GBC=45°,
∴△MGC∽△NGB,
∴![]() =
=![]() ,
,
∴CGNG=BGMG=![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
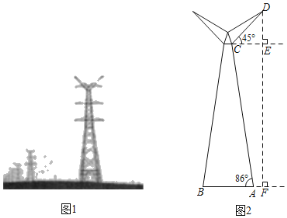
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:

图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____人,扇形统计图中C部分所对应的扇形圆心角的度数为_____;
(2)①补全条形统计图;②若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有多少人;
(3)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
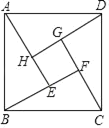
【题目】如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为”赵爽弦图“.已知AE=4,BE=3,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“节能减排,保护环境”,某村计划建造A、B两种型号的沼气池共20个,以解决所有农户的燃料问题.据市场调查:建造A、B两种型号的沼气池各1个,共需费用5万元;建造A型号的沼气池3个,B种型号的沼气池4个,共需费用18万元.
(1)求建造A、B两种型号的沼气池造价分别是多少?
(2)设建造A型沼气池x个,总费用为y万元,求y与x之间的函数关系式;若要使投入总费用不超过52万元,至少要建造A型沼气池多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将牌面数字分别是4,5,6,8的四张扑克牌背面朝上(背面完全相同)洗匀后放在桌面上
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽出一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是8的整数倍的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生身体发育状况,学校抽取一部分学生测量身高(单位:m),绘制处如下的统计图①和图②.请根据相关信息,解答下列问题:
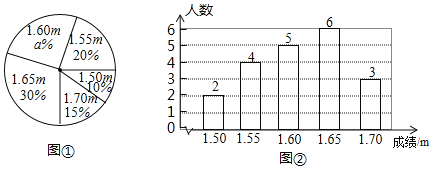
(1)图①中a的值为 ;
(2)求统计的这组学生身高数据的平均数、众数和中位数;
(3)如果全校七年级学生有300人,那么估计身高大于1.65m的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)和B(m,0),且3<m<4,则下列说法:①b<0;②a+c=b;③b2>4ac;④2b>3c;⑤![]() =1,正确的是( )
=1,正确的是( )
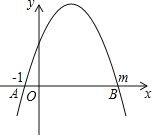
A.①②④B.①③⑤C.②③④D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com