
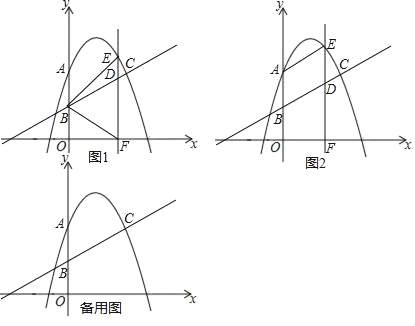
【题目】如图,抛物线y=﹣x2+bx+c经过A(0,3),C(2,n)两点,直线l:y=![]() x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
(1)求抛物线的解析式.
(2)如图1,当点E在直线BC上方的抛物线上运动时,连接BE,BF,是否存在点E使直线BC将△BEF的面积分为2:3两部分?若存在,求出点E的坐标,若不存在说明理由;
(3)如图2,若点E在y轴右侧的抛物线上运动,连接AE,当∠AED=∠ABC时,直接写出此时点E的坐标.
【答案】(1)y=﹣x2+2x+3;(2)存在,E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)点E(
);(3)点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)直线l:y=![]() x+2过C点,则点C(2,3),y=
x+2过C点,则点C(2,3),y=![]() x+2过C点,且与y轴交于点B,则点B(0,2),即可求解;(2)
x+2过C点,且与y轴交于点B,则点B(0,2),即可求解;(2)![]() =
=![]() =
=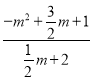 =
=![]() 或
或![]() ,即可求解;(3)分当点E在直线BC上方、点E在直线BC的下方两种情况,分别求解即可.
,即可求解;(3)分当点E在直线BC上方、点E在直线BC的下方两种情况,分别求解即可.
(1)直线l:y=![]() x+2过点C(2,n),且与y轴交于点B,
x+2过点C(2,n),且与y轴交于点B,
∴n=![]() ×2+2=3,当x=0时,y=2,
×2+2=3,当x=0时,y=2,
∴B(0,2),C(2,3)
将点A、C的坐标代入二次函数表达式得:![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)设点E(m,﹣m2+2m+3),则点D(m,![]() m+2),
m+2),
∴DE=﹣m2+![]() m+1,DF=
m+1,DF=![]() m+2,
m+2,
![]() =
=![]() =
=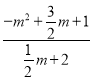 =
=![]() 或
或![]() ,
,
解得:m=![]() 或
或![]() ,
,
∴﹣m2+2m+3=![]() ,或﹣m2+2m+3=
,或﹣m2+2m+3=![]() ,
,
∴点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)由(2)知:E(m,﹣m2+2m+3),则点D(m,![]() m+2),
m+2),
DE=﹣m2+![]() m+1,DF=
m+1,DF=![]() m+2,
m+2,
①如图2,当点E在直线BC上方时,
∵AB∥EF,∠ABD+∠EDB=180°,
∵∠AED=∠ABC,
∴∠AED+∠EDB=180°,
∴AE∥CD,
∴四边形ABDE为平行四边形,
∴AB=DE=1=﹣m2+![]() m+1,
m+1,
解得:m=0或![]() (舍去0);
(舍去0);
∴﹣m2+2m+3=![]() ,即E(
,即E(![]() ,
,![]() ).
).
②如图3,当点E在直线BC的下方时,
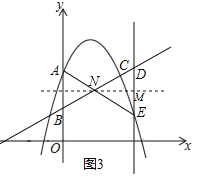
设AE、BD交于点N,过点N作x轴的平行线交DE于点M
∵AB∥DE,
∴∠ABN=∠NDE,而∠AED=∠ABC,
∴∠ABN=∠NDE=∠AED=∠ABC,
∴△NAB、△DEN都是以点N为顶点的等腰三角形,
∴点M的纵坐标和AB中点的坐标同为![]() ,
,
由中点公式得:![]() (﹣m2+2m+3+
(﹣m2+2m+3+![]() m+2)=
m+2)=![]() ,
,
解得:m=0或![]() (舍去0),
(舍去0),
∴﹣m2+2m+3=![]() ,即E(
,即E(![]() ,
,![]() ).
).
综上,点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
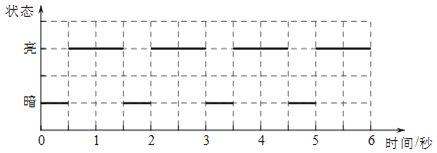
【题目】按《航空障碍灯(MH/T6012﹣1999)》的要求,为保障飞机夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(AviationObstructionlight).中光强航空障碍灯是以规律性的固定模式闪光.在下图中你可以看到某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态的时间总和最长可达__秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
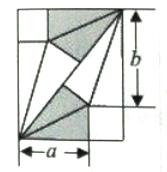
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
电脑型号 | ① | ② | ③ |
工时(个) |
|
|
|
产值(万元) | 0.4 | 0.3 | 0.2 |
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点O是AB边上一点,以O为圆心OB为半径的⊙O与边AB相交于点E,与AC边相切于D点,连接OC交⊙O于点F.
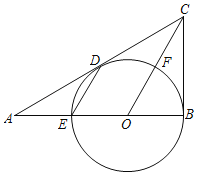
(1)连接DE,求证:OC∥DE;
(2)若⊙O的半径为3.
①连接DF,若四边形OEDF为菱形,弧BD的长为_____(结果保留π)
②若AE=2,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
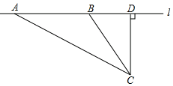
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 得
得![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
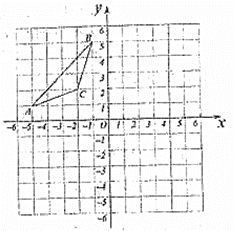
(1)画出![]() 和
和![]() ;
;
(2)![]() ______;
______;
(3)![]() 与
与![]() 组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10的网格中,点A、B、C均在网格线的交点上,
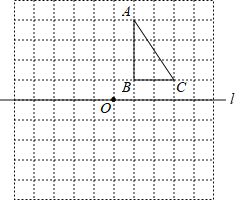
(1)画出△ABC关于直线l对称的△A′B′C′;
(2)画出△ABC绕点O逆时针旋转90°后的△A1B1C1;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com