
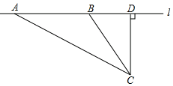
����Ŀ��У����ȫ�ǽ���������ע���ش����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ��ѧ�С����������¼�·����ʻ�������ٶȵ�ʵ�飺���ڹ�·�Ա�ѡȡһ��C�����ڱ�ֱ�ij���l��ȷ����D��ʹCD��l��ֱ�����CD�ij�����24�ף���l�ϵ�D��ͬ��ȡ��A��B��ʹ��CAD��30�㣬��CBD��60�㣮
��1����AB�ij�������������ţ���
��2����֪��·�ζ�У������Ϊ45ǧ��/Сʱ�������ij��У����A��B��ʱ1.5�룬����У���Ƿ��٣�˵�����ɣ����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
���𰸡�(1)![]() ;(2)��У����AB·�γ��٣����ɼ�����.
;(2)��У����AB·�γ��٣����ɼ�����.
��������
��1��������Ǻ����ļ��㹫ʽ���г���ʽ���ֱ����AD��BD�ij��ȣ������������ɡ���2���ڵ�һ�ʵĻ����ϣ����ʱ���ϵ�������ٶȣ��жϣ����ɡ�
�⣺��1��������ã���Rt��ADC�У�tan30�㣽![]() ��
��![]() ��
��
���AD��24![]() ��
��
�� Rt��BDC �У�tan60�㣽![]() ��
��![]() ��
��
���BD��8![]()
����AB��AD��BD��24![]() ��8
��8![]() ��16
��16![]() ���ף���
���ף���
��2��������A��B��ʱ1.5�룬�����ٶ�Ϊ16![]() ��1.5��18.1����/�룩��
��1.5��18.1����/�룩��
��Ϊ18.1����/�룩��65.2ǧ��/ʱ��45ǧ��/ʱ��
���Դ�У����AB·�γ��٣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������C��y��ax2��2ax+3��ֱ��l��y��kx+b����A��B���㣬�ҵ�A��y���ϣ���B��x����������ϣ�
��1�����A�����ꣻ
��2����a����1����ֱ��l�Ľ���ʽ��
��3������3��k����1����a��ȡֵ��Χ��
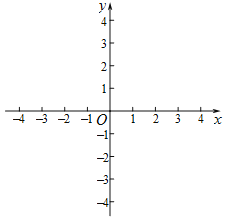
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
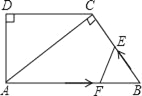
����Ŀ����ͼ����ֱ������ABCD�У�AB��DC����D=90�㣬AC��BC��AB=10cm��BC=6cm��F����2cm/����ٶ����߶�AB����A��B�����˶���E��ͬʱ��1cm/����ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊt�루0��t��5����
��1����֤����ACD�ס�BAC��
��2����DC�ij���
��3�����ı���AFEC�����Ϊy����y����t�ĺ�����ϵʽ�������y����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
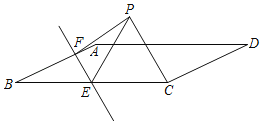
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��4��BC��4![]() ����D��30�㣬��E��BC�ߵ��е㣬F������BA��һ���㣬����BEF��ֱ��EF�۵����õ���PEF������PC������PCEΪ�ȱ�������ʱ��BF�ij�Ϊ_____��
����D��30�㣬��E��BC�ߵ��е㣬F������BA��һ���㣬����BEF��ֱ��EF�۵����õ���PEF������PC������PCEΪ�ȱ�������ʱ��BF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
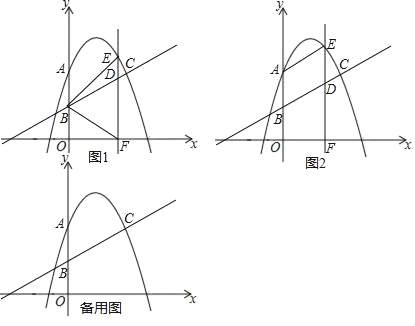
����Ŀ����ͼ��������y����x2+bx+c����A(0��3)��C(2��n)���㣬ֱ��l��y��![]() x+2��C�㣬����y�ύ�ڵ�B������������һ����E������E��ֱ��EF��x���ڵ�F����ֱ��BC�ڵ�D
x+2��C�㣬����y�ύ�ڵ�B������������һ����E������E��ֱ��EF��x���ڵ�F����ֱ��BC�ڵ�D
(1)�������ߵĽ���ʽ��
(2)��ͼ1������E��ֱ��BC�Ϸ������������˶�ʱ������BE��BF���Ƿ���ڵ�Eʹֱ��BC����BEF�������Ϊ2��3�����֣������ڣ������E�����꣬��������˵�����ɣ�
(3)��ͼ2������E��y���Ҳ�����������˶�������AE������AED����ABCʱ��ֱ��д����ʱ��E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=110�㣬��ADE�Ķ���D��BC�ϣ��ҡ�DAE=90�㣬AD=AE�����BAD-��EDC�Ķ���Ϊ�� ��
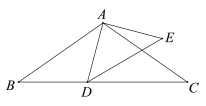
A.17.5��B.12.5��C.12��D.10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��x��0��������A��2��3���͵�B����B�ڵ�A���Ҳࣩ����BC��y�ᣬ����Ϊ��C������AB��AC��AO��BO��
��x��0��������A��2��3���͵�B����B�ڵ�A���Ҳࣩ����BC��y�ᣬ����Ϊ��C������AB��AC��AO��BO��
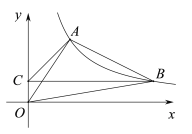
��1����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������ACB=45�㣬��ֱ��AB�Ľ���ʽ��
��3�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() .
.
(1)����������ߵĽ���ʽ��
(2)��![]() ��ÿ��һ����λ���ٶ���
��ÿ��һ����λ���ٶ���![]() ������ƽ�ƣ�ƽ��ʱ��Ϊ
������ƽ�ƣ�ƽ��ʱ��Ϊ![]() �룬ƽ�ƺ��
�룬ƽ�ƺ��![]() ��
��![]() �ص����ֵ����Ϊ
�ص����ֵ����Ϊ![]() ��
��![]() ��
��![]() �غ�ʱֹͣƽ�ƣ���
�غ�ʱֹͣƽ�ƣ���![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(3)��![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ������������ߵĶԳ����ϣ���ֱ��д�����з��������ĵ�
������������ߵĶԳ����ϣ���ֱ��д�����з��������ĵ�![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
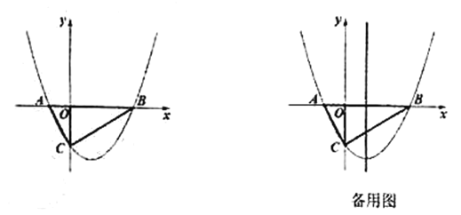
����Ŀ����ͼ��������ABCD�ı߳�Ϊa��E��F�ֱ��DZ�AD��BC���е㣬��G��CD�ϣ���![]() ��DF��EG�ཻ�ڵ�H��
��DF��EG�ཻ�ڵ�H��

��1�����![]() ��ֵ��
��ֵ��
��2����֤��EG��DF��
��3������H��MN��CD���ֱ�AD��BC�ڵ�M��N����P��MN��һ�㣬����P��ʲôλ��ʱ����PDC���ܳ���С�������PDC�ܳ�����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com