
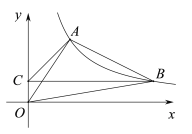
【题目】如图,反比例函数![]() (x>0)经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC,AO,BO.
(x>0)经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC,AO,BO.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若∠ACB=45°,求直线AB的解析式;
(3)求△AOB的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)S△OAB =8.
;(3)S△OAB =8.
【解析】
(1)把A(2,3)代入反比例函数关系式求出k的值即可;
(2)求出点B的坐标,利用待定系数法求出AB的解析式即可;
(3)利用S△OAB=S梯形ABED求解即可.
(1)由题意得,k=xy=2×3=6,
∴反比例函数的解析式为![]() ;
;
(2)如答图,分别过A、B作x轴垂线交x轴于点D、E,AD交BC于点F,
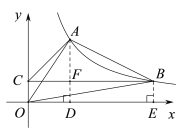
∵∠ACB=45°,点A坐标为(2,3),
∴AF=CF=2,即点C坐标为(0,1),
又BC⊥y轴,
∴点B纵坐标为1,将其带入![]() 得点B坐标为(6,1),
得点B坐标为(6,1),
设直线AB的解析式为y=mx+n,则
![]() ,
,
解得;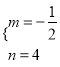 ,
,
∴直线AB的解析式为![]() ;
;
(3)由A(2,3)、B(6,1)知AD=3,BE=1,DE=4,
∵S△OAB=S△OAD+S梯形ABED-S△OBE,且S△OAD= S△OBE,
∴S△OAB=S梯形ABED =![]() ×(BE+AD)×DE=
×(BE+AD)×DE=![]() ×(1+3)×4=8.
×(1+3)×4=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
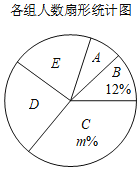
【题目】为了解初一同学们参加学校社团的情况,某班同学随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.其中A:英语演讲社团,B:语文阅读社团,C:数学思维训练社团,D:书法社团,E:天文社团.统计后知道:被调查的同学中数学思维训练社团的学生数是书法社团学生数的1.5倍.
各组人数统计表
组别 | 人数 |
A | 4 |
B | 6 |
C | a |
D | b |
E | 10 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有____人,m=____;
(2)求扇形统计图中扇形D的圆心角度数;
(3)该校共有1000人,请估计参加书法社团的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
电脑型号 | ① | ② | ③ |
工时(个) |
|
|
|
产值(万元) | 0.4 | 0.3 | 0.2 |
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
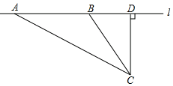
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 得
得![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
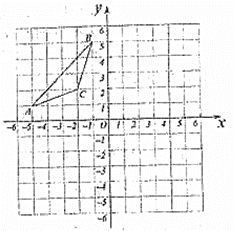
(1)画出![]() 和
和![]() ;
;
(2)![]() ______;
______;
(3)![]() 与
与![]() 组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
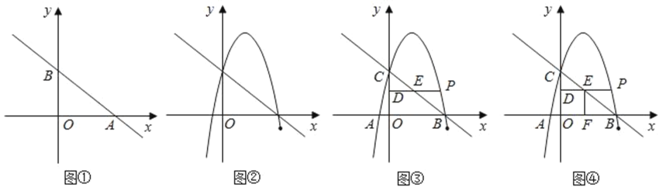
【题目】在平面直角坐标系中,若x轴上的点A与y轴上的点B同时在某函数的图象上则称△AOB为该函数图象的“截距三角形”,如图①,△AOB为直线l的“截距三角形”.
(1)某一次函数图象的“截距三角形”是等腰直角三角形,请写出一个符合条件的函数表达式(写出一个即可);
(2)如图②,若抛物线y=﹣x2+bx+c在第一象限的“截距三角形”与直线y=﹣x+4的“截距三角形”完全重合,求这条抛物线对应的函数表达式;
(3)如图③,在(2)的条件下,在第一象限的抛物线上任取一点P,过点P作x轴的平行线与抛物线在第一象限的“截距三角形”的直角边或直角边的延长线交于点D,与斜边或斜边的延长线交于点E,设点P的横坐标为m,线段DE的长度为d.求d与m之间的函数关系式;
(4)如图④,在(3)的条件下,过点E作EF∥y轴交x轴于点F.求四边形ODEF的周长不变时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
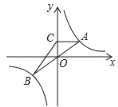
【题目】如图,一直线经过原点O,且与反比例函数y=![]() (k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=_____.
(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com