
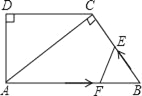
【题目】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
【答案】(1)证明见解析(2)6.4cm(3)当t=![]() 时,y的最小值为19
时,y的最小值为19
【解析】试题分析:(1)由CD∥AB,得∠DCA=∠CAB,加上一组直角,即可证得所求的三角形相似;
(2)在Rt△ABC中,由勾股定理可求得AC的长,根据(1)题所得相似三角形的比例线段,即可求出DC的长;
(3)分析图象可知:四边形AFEC的面积可由△ABC、△BEF的面积差求得,分别求出两者的面积,即可得到y、t的函数关系式,进而可根据函数的性质及自变量的取值范围求出y的最小值.
(1)∵CD∥AB
∴∠BAC=∠DCA
又∵AC⊥BC,∠ACB=90o
∴∠D="∠ACB=" 90o
∴△ACD∽△BAC;
(2)![]()
∵△ACD∽△BAC
∴![]() ,即
,即![]() ,解得:
,解得:![]()
(3)过点E作AB的垂线,垂足为G,

![]()
∴△ACB∽△EGB
∴![]() 即
即![]() ,解得
,解得![]()
![]() =
=![]() =
=![]()
故当t=![]() 时,y的最小值为19
时,y的最小值为19


科目:初中数学 来源: 题型:
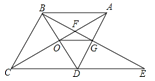
【题目】如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中最小的数为a.


⑴用含a的式子表示这三个数的和;
⑵若这三个数的和是48,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cmB.2.5cm
C.4cmD.5.5cm或2.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:![]()
(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com