
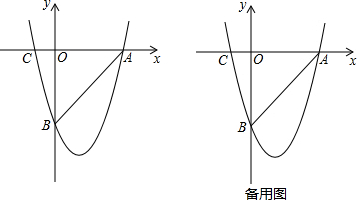
 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点.分析 (1)先根据抛物线y=-x2+2x+3求出抛物线与x轴交点A、B两点坐标,与y轴交点C,以及抛物线的顶点D的坐标,再根据直角坐标系中两点间距离公式求出△BCD三边的长度,再根据勾股定理的逆定理判定△BCD是直角三角形,从而求出∠BCD=90°;
(2)根据点P为抛物线上一动点,且△PAC是直角三角形,分情况讨论:①∠PCA=90°,根据直角坐标系中两直线垂直其斜率(k值)互为负倒数,先求出直线PC的解析式为y=-$\frac{1}{3}$x+3,再利用解析式联立方程组求交点坐标的方法求出点P坐标;②∠PAC=90°,方法同①;③根据题意可知∠APC≠90°.故点P的坐标有两种情况:($\frac{7}{3}$,$\frac{20}{9}$)或($\frac{10}{3}$,$-\frac{13}{9}$).
解答 解:(1)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,即A(-1,0);B(3,0);
当x=0时,y=3,即C(0,3);
抛物线y=-x2+2x+3的顶点坐标为D(1,4);
∵DC=$\sqrt{(1-0)^{2}+(4-3)^{2}}$=$\sqrt{2}$
BC=$\sqrt{(3-0)^{2}+(0-3)^{2}}$=$\sqrt{18}$
BD=$\sqrt{(3-1)^{2}+(0-4)^{2}}$=$\sqrt{20}$
∴DC2+BC2=BD2
∴∠BCD=90°;
(2)设直线AC的解析式为y=kx+b,把点A,C代入得
$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$.
故直线AC的解析式为:y=3x+3
①若∠PCA=90°,则PC⊥AC,所以直线PC的解析式为:y=-$\frac{1}{3}$x+3,
y=-$\frac{1}{3}$x+3与y=-x2+2x+3联立方程组得$\left\{\begin{array}{l}{y=-\frac{1}{3}x+3}\\{y=-{x}^{2}+2x+3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=3}\end{array}\right.$ (舍去),$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{3}}\\{{y}_{2}=\frac{20}{9}}\end{array}\right.$
∴P($\frac{7}{3}$,$\frac{20}{9}$)
②若∠PAC=90°,则PA⊥AC,所以直线PA的解析式为:y=-$\frac{1}{3}$x+n
把点A(-1,0)代入得n=-$\frac{1}{3}$.
故y=-$\frac{1}{3}$x$-\frac{1}{3}$
y=-$\frac{1}{3}$x$-\frac{1}{3}$与y=-x2+2x+3联立方程组得
$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{1}{3}}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$ (舍去),$\left\{\begin{array}{l}{{x}_{2}=\frac{10}{3}}\\{{y}_{2}=-\frac{13}{9}}\end{array}\right.$
故P($\frac{10}{3}$,$-\frac{13}{9}$)
③根据题意可知∠APC≠90°.
综上可知点P的坐标为($\frac{7}{3}$,$\frac{20}{9}$)或($\frac{10}{3}$,$-\frac{13}{9}$).
点评 本题主要考查了二次函数的图象上一些特殊点的求法即应用.第(1)问根据直角坐标系中两点间距离公式AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$求线段的长度,再利用勾股定理的逆定理判定直角三角形是解决此类问题的关键;第(2)问根据直角三角形的性质求动点坐标,若题目中没有给定直角应该分情况讨论.利用直角坐标系中两直线垂直其斜率(k值)互为负倒数的方法求直线解析式的方法要掌握,可以简化计算.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
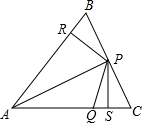 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上).
如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是12米.
颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是12米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com