
【题目】在△ABC中,F是BC上一点,FG⊥AB,垂足为G.
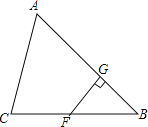
(1)过C点画CD⊥AB,垂足为D;
(2)过D点画DE∥BC,交AC于E;
(3)求证:∠EDC=∠GFB.
【答案】见解析
【解析】
试题分析:(1)以C为圆心画弧,与AB交于两点,分别以两点为圆心,大于两点距离一半长为半径画弧,两弧交于一点,作出垂直CD即可;
(2)以D为顶点,作∠ADE=∠B,利用同位角相等两直线平行即可确定出DE;
(3)由FG与CD都与AB垂直,得到FG与CD平行,利用两直线平行同位角相等得到一对角相等,再由DE与BC平行,得到一对内错角相等,等量代换即可得证.
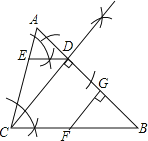
解:(1)画CD⊥AB,如图所示;
(2)画DE∥BC,如图所示;
(3)证明:∵FG⊥AB,CD⊥AB,
∴∠FGB=∠CDB=90°,
∴FG∥CD,
∴∠DFB=∠DCB,
∵DE∥BC,
∴∠EDC=∠DCB,
∴∠EDC=∠GFB.


科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
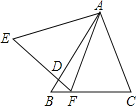
①∠AFC=∠C;
②DE=CF;
③△ADE∽△FDB;
④∠BFD=∠CAF
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你写出勾股定理内容(用文字语言表述):
[尝试证明]
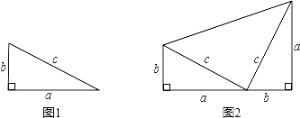
以图1中的直角三角形为基础,可以构造出以a、b为底,以(a+b)为高的直角梯形(如图2),请你利用图2,证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题
(1)解下列方程组(直接写出方程组的解即可)
①![]() 的解为 ②
的解为 ②![]() 的解为 ③
的解为 ③![]() 的解为
的解为
(2)以上每个方程组的解中,x值与y值的大小关系为 .
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆锥的主视图是边长为4 cm的等边三角形,则该圆锥俯视图的面积是( )
A. 4cm2 B. 8 cm2 C. 12 cm2 D. 16 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图像反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图像回答下列问题:
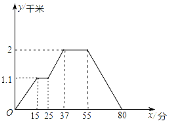
(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
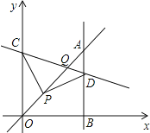
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(![]() ,
,![]() ) B.(3,3) C. (
) B.(3,3) C. (![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
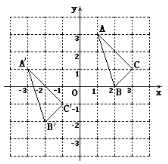
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标:![]() ;
; ![]() ;
;![]() ;
;
⑵说明![]() 由
由![]() 经过怎样的平移得到? .
经过怎样的平移得到? .
⑶若点![]() (
(![]() ,
,![]() )是
)是![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ;
的坐标为 ;
⑷求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com