
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标:![]() ;
; ![]() ;
;![]() ;
;
⑵说明![]() 由
由![]() 经过怎样的平移得到? .
经过怎样的平移得到? .
⑶若点![]() (
(![]() ,
,![]() )是
)是![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ;
的坐标为 ;
⑷求![]() 的面积.
的面积.
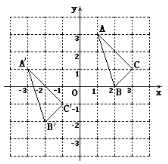
【答案】(1)、A′(-3,1);B′(-2,-2);C′(-1,-1);(2)、先向左平移4个单位,再向下平移2个单位;(3)、P′(a-4,b-2);(4)、2.
【解析】
试题分析:(1)、根据点所在的位置得出坐标;(2)、根据对应点得出图象的平移法则;(3)、根据平移法则得出点的坐标;(4)、利用矩形的面积减去3个直角三角形的面积求出△ABC的面积.
试题解析:(1)、A′(-3,1);B′(-2,-2);C′(-1,-1)
(2)、将△ABC先向左平移4个单位,再向下平移2个单位得到△A′B′C′.
(3)、P′(a-4,b-2)
(4)、S=2×3-1×3÷2-2×2÷2-1×1÷2=6-1.5-2-0.5=2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,F是BC上一点,FG⊥AB,垂足为G.
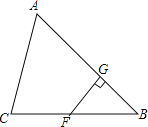
(1)过C点画CD⊥AB,垂足为D;
(2)过D点画DE∥BC,交AC于E;
(3)求证:∠EDC=∠GFB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,AC=BC,BM⊥CM于M,且CM>BM
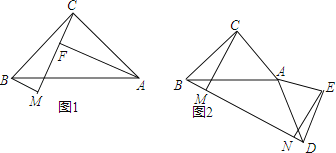
(1)如图1,过点A作AF⊥CM于F,直线写出线段BM、AF、MF的数量关系是
(2)如图2,D为BM延长线上一点,连AD以AD为斜边向右侧作等腰Rt△ADE,再过点E作EN⊥BM于N,求证:CM+EN=MN;
(3)将(2)中的△ADE绕点A顺时针旋转任意角α后,连BD取BD中点P,连CP、EP,作出图形,试判断CP、EP的数量和位置关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.
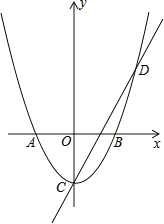
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G、P、Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com