
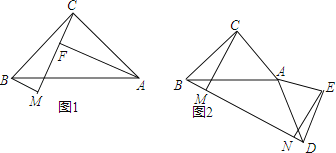
【题目】已知在Rt△ABC中,∠ACB=90°,AC=BC,BM⊥CM于M,且CM>BM
(1)如图1,过点A作AF⊥CM于F,直线写出线段BM、AF、MF的数量关系是
(2)如图2,D为BM延长线上一点,连AD以AD为斜边向右侧作等腰Rt△ADE,再过点E作EN⊥BM于N,求证:CM+EN=MN;
(3)将(2)中的△ADE绕点A顺时针旋转任意角α后,连BD取BD中点P,连CP、EP,作出图形,试判断CP、EP的数量和位置关系并证明.
【答案】(1)AF=BM+MF.(2)证明见解析;(3)CP=PE且CP⊥PE.
【解析】
试题分析:(1)根据全等三角形的判定定理AAS推知△ACF≌△CBM,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换,即可解答;
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,由四边形GMNH为矩形,得到AH⊥EN,根据三垂直得:△CMB≌△AGC,△AEH≌△EDN,利用全等三角形的对应边相等得到相等的线段,即可解答.
(3)取AB的中点M、AD的中点N,连接PM、CM、NE、PN,则可构造△PNE≌CMP,结论不言而喻.
解:(1)AF=BM+MF,
∵∠ACB=90°,
∴∠ACF+∠BCM=90°.
又∵AF⊥CM,
∴∠ACF+∠CAF=90°,
∴∠CAF=∠BCM.
在△ACF和△CBM中,
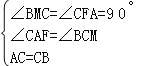 ,
,
∴△ACF≌△CBM,
∴BM=CF,AF=CM,
∴CF+MF=BM+MF=MC=AF,即AF=BM+MF.
故答案为:AF=BM+MF.
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,
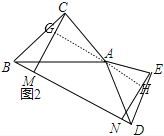
∴四边形GMNH为矩形
∴AH⊥EN
根据三垂直得:△CMB≌△AGC,△AEH≌△EDN,
∴CM=AG,EN=AH,
∴MN=GH=GA+AH=CM+EN.
(3)如图3,
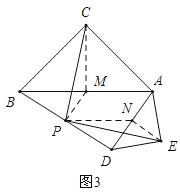
取AB的中点M、AD的中点N,连接PM、CM、NE、PN,
∵△BCA与△AED均为等腰直角三角形,
∴CM=BM=AM,CM⊥BA,
EN=AN=DN,NE⊥AD,
∵P为BD中点,
∴PN=AM=BM=CM,PN∥BA,
PM=AN=DN=NE,PM∥AD,
∴AMPN是平行四边形,
∴∠BMP=∠PND,
∴∠PMC=∠ENP,
∴△PNE≌CMP(SAS),
∴CP=PE,
∵CM⊥AB,PN∥AB,
∴CM⊥PN,
∴CP⊥PE,
综上所述,CP=PE且CP⊥PE.


科目:初中数学 来源: 题型:
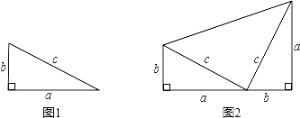
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你写出勾股定理内容(用文字语言表述):
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以(a+b)为高的直角梯形(如图2),请你利用图2,证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
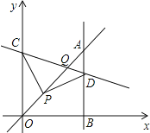
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(![]() ,
,![]() ) B.(3,3) C. (
) B.(3,3) C. (![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,正确的是( )
A. 3m+2n=5mn B. 4a2+3a3=7a5 C. 5a2b-3ba2=2a2b D. 5a2-4a2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
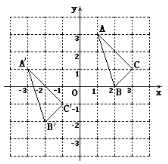
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标:![]() ;
; ![]() ;
;![]() ;
;
⑵说明![]() 由
由![]() 经过怎样的平移得到? .
经过怎样的平移得到? .
⑶若点![]() (
(![]() ,
,![]() )是
)是![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ;
的坐标为 ;
⑷求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
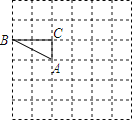
(1)画出旋转后的△AB′C′;
(2)以点C为坐标原点,线段BC、AC所在直线分别为x轴,y轴建立直角坐标系,请直接写出点B′的坐标 ;
(3)写出△ABC在旋转过程中覆盖的面积 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com