
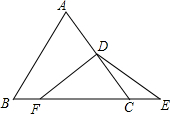
 如图,△ABC是等边三角形,若D是边AC上的任意点,延长BC至E,DF=DE.请猜想AD,BF,CE之间的数量关系,并证明.
如图,△ABC是等边三角形,若D是边AC上的任意点,延长BC至E,DF=DE.请猜想AD,BF,CE之间的数量关系,并证明. 分析 作DM⊥BC于M,则∠DMC=90°,由等边三角形的性质得出AC=BC,∠ACB=60°,得出∠MDC=30°,由含30°角的直角三角形的性质得出2CD=2CM,由等腰三角形的性质得出FM=EM,即可得出结论.
解答 解:BF+CE=AD;理由如下: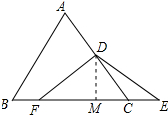
作DM⊥BC于M,则∠DMC=90°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠MDC=30°,
∴2CD=2CM,
∵DF=DE,
∴FM=EM,
∴BF+CE=BC-CF+ME-CM=AC-FM-CM+ME-CM=AC-2CM=AC-CD=AD.
点评 本题考查了等边三角形的性质、等腰三角形的性质、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,通过作辅助线运用等腰三角形和直角三角形的性质是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
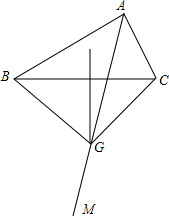 如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论.
如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
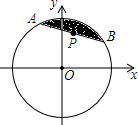 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )| A. | π-1 | B. | π-2 | C. | $\frac{4π}{3}$-1 | D. | $\frac{4π}{3}$-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-8)2=3 | B. | (x-4)2=3 | C. | (x-4)2=19 | D. | (x-4)2=13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com