
 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB=2$\sqrt{2}$,∠BCD=30°,则⊙O的半径为$\frac{2\sqrt{6}}{3}$.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB=2$\sqrt{2}$,∠BCD=30°,则⊙O的半径为$\frac{2\sqrt{6}}{3}$. 分析 连接OB,根据垂径定理求出BE,求出∠BOE=60°,解直角三角形求出OB即可.
解答 解: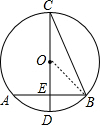
连接OB,
∵OC=OB,∠BCD=30°,
∴∠BCD=∠CBO=30°,
∴∠BOE=∠BCD+∠CBO=60°,
∵直径CD⊥弦AB,AB=2$\sqrt{2}$,
∴BE=$\frac{1}{2}$AB=$\sqrt{2}$,∠OEB=90°,
∴OB=$\frac{BE}{sin60°}$=$\frac{2\sqrt{6}}{3}$,
即⊙O的半径为$\frac{2\sqrt{6}}{3}$,
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题考查了垂径定理,等腰三角形的性质,解直角三角形,三角形外角性质的应用,能根据垂径定理求出BE和解直角三角形求出OB长是解此题的关键,难度适中.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小云玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字-1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).
小云玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字-1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥$-\frac{1}{4}$ | B. | m≤$-\frac{1}{4}$ | C. | m≥$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
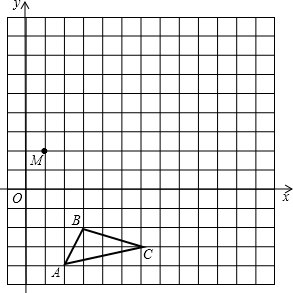 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com