
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=aЃЈx-1ЃЉ2+4гыxжсНЛгкЕуAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЕуPдкетЬѕХзЮяЯпЩЯЃЌЧвВЛгыBЁЂCСНЕужиКЯЃЎЙ§ЕуPзїyжсЕФДЙЯпгыЩфЯпBCНЛгкЕуQЃЌвдPQЮЊБпзїRtЁїPQFЃЌЪЙЁЯPQF=90ЁуЃЌЕуFдкЕуQЕФЯТЗНЃЌЧвQF=1ЃЎЩшЯпЖЮPQЕФГЄЖШЮЊdЃЌЕуPЕФКсзјБъЮЊmЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=aЃЈx-1ЃЉ2+4гыxжсНЛгкЕуAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЕуPдкетЬѕХзЮяЯпЩЯЃЌЧвВЛгыBЁЂCСНЕужиКЯЃЎЙ§ЕуPзїyжсЕФДЙЯпгыЩфЯпBCНЛгкЕуQЃЌвдPQЮЊБпзїRtЁїPQFЃЌЪЙЁЯPQF=90ЁуЃЌЕуFдкЕуQЕФЯТЗНЃЌЧвQF=1ЃЎЩшЯпЖЮPQЕФГЄЖШЮЊdЃЌЕуPЕФКсзјБъЮЊmЃЎЗжЮі ЃЈ1ЃЉАбЕуBЃЈ3ЃЌ0ЃЉДњШыХзЮяЯпy=aЃЈx-1ЃЉ2+4ЃЌЧѓГіaЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЯШЧѓГіжБЯпBCЕФНтЮіЪНЃЌгЩЕуQЕФзнзјБъЧѓГіКсзјБъЃЌЧѓГіPQЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉгЩЬтвтЕУГіЕуPгыЕуQЙигкyжсЖдГЦЃЌЕУГіЗНГЬЃЌНтЗНГЬМДПЩЃЛ
ЃЈ4ЃЉЗжСНжжЧщПіЃКЂйЕБЕуFТфдкЁїOBDЕФжБНЧБпЩЯЪБЃЌбгГЄQFНЛOBгкGЃЌжЄГіЁїOFGЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіOG=FGЃЌгЩFG=QG-QFЃЌЕУГіЗНГЬЃЌНтЗНГЬМДПЩЃЛ
ЂкЕБЕуFТфдкЁїOBDЕФаББпЩЯЪБЃЌжЄГіЁїBQFЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіBF=QF=1ЃЌOF=2ЃЌЕУГіЗНГЬЃЌНтЗНГЬМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉАбЕуBЃЈ3ЃЌ0ЃЉДњШыХзЮяЯпy=aЃЈx-1ЃЉ2+4ЃЌ
ЕУЃК4a+4=0ЃЌ
НтЕУЃКa=-1ЃЌ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКy=-ЃЈx-1ЃЉ2+4=-x2+2x+3ЃЌ
МДХзЮяЯпНтЮіЪНЮЊЃКy=-x2+2x+3ЃЛ
ЃЈ2ЃЉЖдгкХзЮяЯпy=-x2+2x+3ЃЌ
ЕБx=0ЪБЃЌy=3ЃЛ
ЕБy=0ЪБЃЌx=-1ЃЌЛђx=3ЃЌ
ЁрCЃЈ0ЃЌ3ЃЉЃЌAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊЃКy=kx+bЃЌ
ИљОнЬтвтЕУЃК$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$ЃЌ
НтЕУЃКk=-1ЃЌb=3ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊЃКy=-x+3ЃЌ
ЁпЕуPЕФзјБъЮЊЃКЃЈmЃЌ-m2+2m+3ЃЉЃЌ
ЁрЕуQЕФзнзјБъзјБъЮЊЃК-m2+2m+3ЃЌ
дђ-x+3=-m2+2m+3ЃЌx=m2-2mЃЌ
ЁрЕуQЕФзјБъЮЊЃЈm2-2mЃЌ-m2+2m+3ЃЉЃЌ
ЁрЕБ-1ЁмmЃМ0ЪБЃЌШчЭМ1ЃЌ
d=m2-2m-m=m2-3mЃЌ
ЕБ0ЃМmЃМ3ЪБЃЌШчЭМ2ЃЌ
d=m-ЃЈm2-2mЃЉ=-m2+3m
ЁрdгыmжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃКd=$\left\{\begin{array}{l}{{m}^{2}-3mЃЈ-1ЁмmЃМ0ЃЉ}\\{-{m}^{2}+3mЃЈ0ЃМmЃМ3ЃЉ}\end{array}\right.$ЃЛ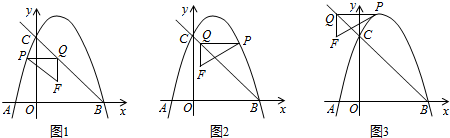
ЃЈ3ЃЉЕБRtЁїPQFЕФБпPFБЛyжсЦНЗжЪБЃЌЕуPгыЕуQЙигкyжсЖдГЦЃЌ
ЁрКсзјБъЛЅЮЊЯрЗДЪ§ЃЌ
Ёрm2-2m+m=0ЃЌ
НтЕУЃКm=1ЃЌЛђm=0ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
Ёрm=1ЃЌ
Ёрd=3-1=2ЃЛ
ЃЈ4ЃЉЗжЫФжжЧщПіЃК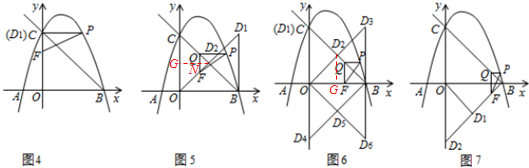
ЂйЧщаЮвЛЃКШчЭМ4ЫљЪОЃЌ
ЁпCЕуЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
НЋy=3ДњШыКЏЪ§y=-x2+2x+3ЕУx1=0ЃЈЩсШЅЃЉЃЌx2=2ЃЌ
ЁрPЕуЕФКсзјБъm=2ЃЛ
ЂкЧщаЮЖўЃКШчЭМ5ЫљЪОЃКЙ§D2ЕузїD2GЁЭCOНЛQFгыNЕуЃЌ
ЁпBЃЈ3ЃЌ0ЃЉ
ЁрD2ЃЈ$\frac{3}{2}$ЃЌ$\frac{3}{2}$ЃЉЃЌ
ЁпCO=3ЃЌQF=1ЃЌQFЁЮCOЃЌ
Ёр$\frac{{D}_{2}N}{{D}_{2}G}$=$\frac{QF}{CO}$ЃЌ
ЁрD2N=$\frac{1}{2}$ЃЌ
ЁрQЃЈ1ЃЌ2ЃЉЃЌ
НЋy=2ДњШыКЏЪ§y=-x2+2x+3ЕУx1=1+$\sqrt{2}$ЃЌx2=1-$\sqrt{2}$ЃЈЩсШЅЃЉЃЌ
Ёрm=1+$\sqrt{2}$ЃЛ
ЂлЧщаЮШ§ЃКШчЭМ6ЫљЪОЃКЙ§D2ЕузїD2GЁЭOBЃЌ
ЁпBЃЈ3ЃЌ0ЃЉ
ЁрD2ЃЈ$\frac{3}{2}$ЃЌ$\frac{3}{2}$ЃЉЃЌ
ЁпBG=$\frac{3}{2}$ЃЌQF=1ЃЌQFЁЮCOЃЌ
Ёр$\frac{QF}{{D}_{2}G}=\frac{BF}{BG}$ЃЌ
ЁрBF=1ЃЌ
ЁрQЃЈ1ЃЌ1ЃЉЃЌ
НЋy=1ДњШыКЏЪ§y=-x2+2x+3ЕУx1=1+$\sqrt{3}$ЃЌx2=1-$\sqrt{3}$ЃЈЩсШЅЃЉЃЌ
Ёрm=1+$\sqrt{3}$ЃЛ
ЂмЧщаЮЫФЃКШчЭМ7ЫљЪОЃК
ЁпCD4=6ЃЌQF=1ЃЌBC=3$\sqrt{2}$ЃЌЧвQFЁЮCD2ЃЌ
Ёр$\frac{BQ}{BC}=\frac{QF}{C{D}_{2}}$ЃЌ
ЁрBQ=$\frac{\sqrt{2}}{2}$ЃЌ
ЁрQЕузнзјБъЮЊ$\frac{1}{2}$ЃЌМДPЕузнзјБъЃЌ
НЋy=$\frac{1}{2}$ДњШыКЏЪ§y=-x2+2x+3ЕУx1=$\frac{2+\sqrt{14}}{2}$ЃЌx2=$\frac{2-\sqrt{14}}{2}$ЃЈЩсШЅЃЉЃЌ
Ёрm=$\frac{2+\sqrt{14}}{2}$ЃЎ
злЩЯЫљЪіЃКЕБ0ЃМmЃМ3ЪБЃЌЕуFТфдкЁїOBDЕФБпЩЯЪБmЕФжЕЮЊЃК2ЃЌЛђ1+$\sqrt{2}$ЃЌЛђ1+$\sqrt{3}$ЃЌЛђ$\frac{2+\sqrt{14}}{2}$ЃЎ
ЕуЦР БОЬтЪЧЖўДЮКЏЪ§злКЯЬтФПЃЌПМВщСЫЖўДЮКЏЪ§НтЮіЪНЕФЧѓЗЈЁЂжсЖдГЦЕФаджЪЁЂгУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНЁЂЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЁЂвЛдЊЖўДЮЗНГЬЕФНтЗЈЕШжЊЪЖЃЛБОЬтФбЖШНЯДѓЃЌзлКЯадЧПЃЌЬиБ№ЪЧЃЈ4ЃЉжаЃЌашвЊНјааЗжРрЬжТлЃЌЛГіЭМаЮЃЌжЄУїЕШбќжБНЧШ§НЧаЮКЭНтвЛдЊЖўДЮЗНГЬВХФмЕУГіНсЙћЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
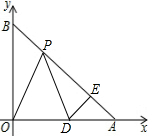 вбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈaЁЂoЃЉЁЂBЃЈoЁЂbЃЉТњзу$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0ЃЌPЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌDЪЧxжсе§АыжсЩЯвЛЕуЃЌЧвPO=PDЃЌDEЁЭABгкEЃЎ
вбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈaЁЂoЃЉЁЂBЃЈoЁЂbЃЉТњзу$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0ЃЌPЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌDЪЧxжсе§АыжсЩЯвЛЕуЃЌЧвPO=PDЃЌDEЁЭABгкEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌЕуDдкЁїABCЕФБпBCЩЯЃЌЁЯC+ЁЯBAD=ЁЯDACЃЌtanЁЯBAD=$\frac{4}{7}$ЃЌAD=$\sqrt{65}$ЃЌCD=13ЃЌдђЯпЖЮACЕФГЄЮЊ4$\sqrt{13}$ЃЎ
ШчЭМЃЌЕуDдкЁїABCЕФБпBCЩЯЃЌЁЯC+ЁЯBAD=ЁЯDACЃЌtanЁЯBAD=$\frac{4}{7}$ЃЌAD=$\sqrt{65}$ЃЌCD=13ЃЌдђЯпЖЮACЕФГЄЮЊ4$\sqrt{13}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯBAD=ЁЯADC=90ЁуЃЌAB=AD=2$\sqrt{2}$ЃЌCD=$\sqrt{2}$ЃЌЕуPдкЫФБпаЮABCDЕФБпЩЯЃЎШєЕуPЕНBDЕФОрРыЮЊ$\frac{3}{2}$ЃЌдђЕуPЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯBAD=ЁЯADC=90ЁуЃЌAB=AD=2$\sqrt{2}$ЃЌCD=$\sqrt{2}$ЃЌЕуPдкЫФБпаЮABCDЕФБпЩЯЃЎШєЕуPЕНBDЕФОрРыЮЊ$\frac{3}{2}$ЃЌдђЕуPЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 2 | BЃЎ | 3 | CЃЎ | 4 | DЃЎ | 5 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 880дЊ | BЃЎ | 800дЊ | CЃЎ | 720дЊ | DЃЎ | 1080дЊ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | a3+a3=2a6 | BЃЎ | ЃЈx2ЃЉ3=x5 | CЃЎ | 2a6ЁТa3=2a2 | DЃЎ | x3•x2=x5 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌдкЁбOжаЃЌCDЪЧжБОЖЃЌЯвABЁЭCDЃЌДЙзуЮЊEЃЌСЌНгBCЃЎШєAB=2$\sqrt{2}$ЃЌЁЯBCD=30ЁуЃЌдђЁбOЕФАыОЖЮЊ$\frac{2\sqrt{6}}{3}$ЃЎ
ШчЭМЃЌдкЁбOжаЃЌCDЪЧжБОЖЃЌЯвABЁЭCDЃЌДЙзуЮЊEЃЌСЌНгBCЃЎШєAB=2$\sqrt{2}$ЃЌЁЯBCD=30ЁуЃЌдђЁбOЕФАыОЖЮЊ$\frac{2\sqrt{6}}{3}$ЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com