
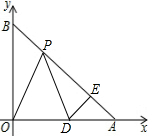
 已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.分析 (1)根据已知等式,利用非负数的性质求出a与b的值即可;
(2)当P点运动时,PE的值不变化,PE=3,理由为:过O作OC垂直于AB,由OA=OB,C为斜边AB的中点,利用勾股定理求出AB的长,利用斜边上的中线等于斜边的一半求出OC的长,再由三角形AOB为等腰直角三角形,得到AC=BC,且∠AOC=∠BOC=45°,根据PO=PD,利用等边对等角得到一对角相等,利用外角性质及等式性质得到一对角相等,再由一对直角相等,且PO=PD,利用AAS得到三角形POC与三角形DPE全等,利用全等三角形对应边相等得到PE=OC,求出PE的长即可;
(3)由∠OPD度数及PO=PD,利用等边对等角及内角和定理求出∠POD与∠PDO的度数,利用外角性质得到一对角相等,利用AAS得到三角形POB与三角形PDA全等,利用全等三角形对应边相等得到OB=PA=OA,根据OA-AD求出OD的长,即可确定出D的坐标.
解答 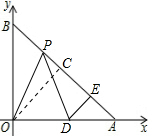 解:(1)∵$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,
解:(1)∵$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,
∴$\left\{\begin{array}{l}{a-b=0}\\{a-3\sqrt{2}=0}\end{array}\right.$,
解得:a=b=3$\sqrt{2}$;
(2)当P点运动时,PE的值不变化,PE=3,理由为:
过O作OC⊥AB,
∵OA=OB=3$\sqrt{2}$,C为斜边AB的中点,
∴AB=$\sqrt{({3\sqrt{2})}^{2}+(3\sqrt{2})^{2}}$=6,即OC=$\frac{1}{2}$AB=3,
∵△AOB为等腰直角三角形,
∴AC=BC,∠AOC=∠BOC=45°,
∵PO=PD,
∴∠POD=∠PDO,
∵∠POD=45°+∠POC,∠PDO=45°+∠APD,
∴∠POC=∠APD,
在△POC和△DPE中,
$\left\{\begin{array}{l}{∠POC=∠PDE}\\{∠PCO=∠DEP=90°}\\{PO=PD}\end{array}\right.$,
∴△POC≌△DPE(AAS),
∴OC=PE=3;
(3)∵OP=DP,∠OPD=45°,
∴∠POD=∠PDO=$\frac{180°-45°}{2}$=67.5°,
∴∠PDA=180°-∠PDO=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO,
在△POB和△DPA中,
$\left\{\begin{array}{l}{∠BPO=∠PDA}\\{∠OBP=∠PAD}\\{OA=OB}\end{array}\right.$,
∴△POB≌△DPA(AAS),
∴OB=PA=OA=3$\sqrt{2}$,
∴DA=PB=6-3$\sqrt{2}$,
∴OD=OA-DA=3$\sqrt{2}$-(6-3$\sqrt{2}$)=6$\sqrt{2}$-6,
则D(6$\sqrt{2}$-6,0).
点评 此题属于一次函数综合题,涉及的知识有:全等三角形的判定与性质,非负数的性质,外角性质及内角和定理,坐标与图形性质,以及等腰三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
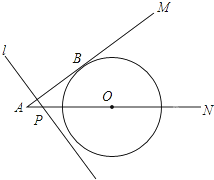 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒.
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
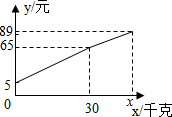 一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:
一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
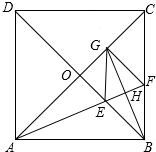 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF于点H,交AC于点G,连接GE、GF.
如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF于点H,交AC于点G,连接GE、GF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
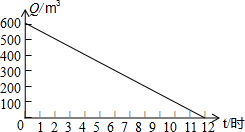 河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.
河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
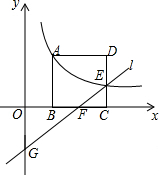 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com