
分析 令函数y1=(x-a)(x-a2)-(x-a3)、y2=(x-a2)(x-a3)-(x-a)、y3=(x-a3)(x-a)-(x-a2),可知三个函数均为二次项系数为正的二次函数,若a>1知1<a<a2<a3,继而可得x=a2时y2<0、x=a3时y3<0,即第一、三两个方程有实数根,同理可判断0<a<1时方程的根的情况.
解答 解:设a>1,1<a<a2<a3,令函数
y1=(x-a)(x-a2)-(x-a3),
y2=(x-a2)(x-a3)-(x-a),
y3=(x-a3)(x-a)-(x-a2),
三个函数均为二次项系数为正的二次函数,
当x=a2时,y2=a-a2=a(1-a)<0,
当x=a3时,y3=a2-a3=a2(1-a)<0,
∴方程(x-a2)(x-a3)=x-a、(x-a3)(x-a)=x-a2存在实数根;
设0<a<1,0<a3<a2<a<1,
当x=a时,y1=-a+a3=a(a2-1)<0,
当x=a时,y3=-a+a2=a(a-1)<0,
∴方程(x-a)(x-a2)=x-a3、(x-a3)(x-a)=x-a2存在实数根;
综上,三个方程(x-a)(x-a2)=x-a3,(x-a2)(x-a3)=x-a,(x-a3)(x-a)=x-a2中至少有两个方程存在实数根.
点评 本题主要考查方程的根的情况,将判断一元二次方程根的情况转化为判断二次函数与x轴交点情况来求是解题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
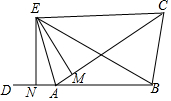 如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.
如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com