
【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
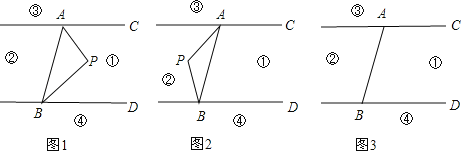
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
【答案】(1)证明解解析(2)不成立(3)(a)当动点P在射线BA的右侧时,结论是:∠PBD=∠PAC+∠APB.(b)当动点P在射线BA上,结论是:∠PBD=∠PAC+∠APB.或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可).(c)当动点P在射线BA的左侧时,结论是∠PAC=∠APB+∠PBD.选择(a)证明见解析
【解析】
试题分析:(1)如图1,延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
解:(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
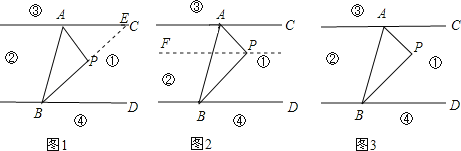
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是:
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,结论是:
∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
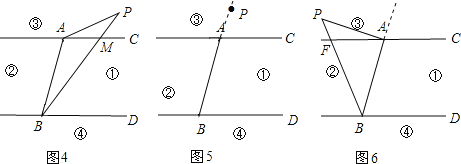
选择(a)证明:
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.


科目:初中数学 来源: 题型:
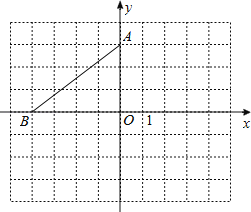
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
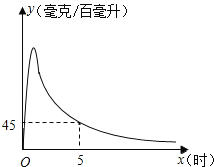
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
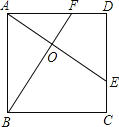
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
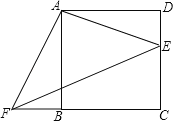
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com